题目内容
已知半径为R的球的体积公式为V球=
πR3,若在半径为R的球O内任取一点P,则点P到球心O的距离不大于
的概率为
.
| 4 |
| 3 |
| R |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |
分析:本题利用几何概型求解.先根据到点O的距离不大于
的点构成图象特征,求出其体积,最后利用体积比即可得所求的概率.
| R |
| 2 |
解答:解:∵到点O的距离不大于
的点构成一个球体,其半径为
,
则点P到点O的距离不大于
的概率为:
P=
=(
)3=
故答案为:
.
| R |
| 2 |
| R |
| 2 |
则点P到点O的距离不大于
| R |
| 2 |
P=
| 小球的体积 |
| 大球的体积 |
| ||
| R |
| 1 |
| 8 |
故答案为:
| 1 |
| 8 |
点评:本小题主要考查几何概型、球的体积等基础知识,考查运算求解能力,考查空间想象力、化归与转化思想.属于基础题.

练习册系列答案
相关题目

 ,若在半径为R的球O内任取一点P,则点P到球心O的距离不大于
,若在半径为R的球O内任取一点P,则点P到球心O的距离不大于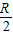 的概率为 .
的概率为 .