题目内容

设α，β∈(-
π
2
，
π
2
)，那么“α＜β”是“tanα＜tanβ”的（　　）
A、充分页不必要条件
B、必要而不充分条件
C、充分必要条件
D、既不充分也不必要条件
分析：根据函数y=tanx在区间(-
π
2
，
π
2
)的单调性可解题．
解答：解：在开区间(-
π
2
，
π
2
)中，函数y=tanx为单调增函数，
所以设α，β∈(-
π
2
，
π
2
)，
那么“α＜β”是“tanα＜tanβ”的充分必要条件，
故选C．
点评：本题主要考查正切函数的单调性问题．属基础题．
练习册系列答案
相关题目
设a=30.2，b=log
1
2
π，c=(
1
2
)0..3，则a，b，c从大到小的顺序为
a＞c＞b
a＞c＞b
．
在数列{an}中，a1=1，an+1=
1
2
an +n，n为奇数
an-2n，n为偶数
，设bn=a2n-2，Sn=|b1|+|b2|+…+|bn|．
（1）求数列{bn}的通项公式；
（2）若Tn=a1+a2+a3+…+a2n+a2n+1，试比较Sn与Tn的大小．
设复数z1=2-i，z2=m+i（m∈R，i为虚数单位），若z1•z2为实数，则m的值为
 
．
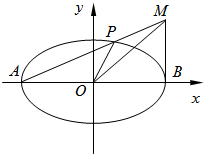精英家教网如图，已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)，A、B是长轴的左、右端点，动点M满足MB⊥AB，联结AM，交椭圆于点P．
（1）当a=2，b=
2
时，设M（2，2），求
OP
•
OM
的值；
（2）若
OP
•
OM
为常数，探究a、b满足的条件？并说明理由；
（3）直接写出
OP
•
OM
为常数的一个不同于（2）结论类型的几何条件．
设
a
=（2，4），
b
=（1，1），若
b
⊥（
a
+m
b
），则实数m=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网