题目内容
【题目】已知函数![]() ,其中
,其中![]() 均为实数,
均为实数, ![]() 为自然对数的底数.
为自然对数的底数.
(I)求函数![]() 的极值;
的极值;
(II)设![]() ,若对任意的
,若对任意的![]() ,
,
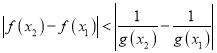 恒成立,求实数
恒成立,求实数![]() 的最小值.
的最小值.
【答案】(1)当![]() 时,
时, ![]() 取得极大值
取得极大值![]() ,无极小值;(2)
,无极小值;(2)![]() .
.
【解析】试题分析:(1)由题对![]() 得
得![]() ,研究其单调性,可得当
,研究其单调性,可得当![]() 时,
时, ![]() 取得极大值
取得极大值![]() ,无极小值;
,无极小值;
(2)由题当![]() 时,
时, ![]() ,由单调性可得
,由单调性可得![]() 在区间
在区间![]() 上为增函数,根据
上为增函数,根据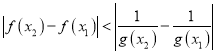 ,构造函数
,构造函数![]() ,
,
由单调性可得![]() 在区间
在区间![]() 上为增函数,不妨设
上为增函数,不妨设![]() ,
,
则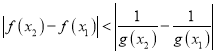 等价于
等价于![]() ,
,
即![]() ,
,
故又构造函数![]() ,
,
可知![]() 在区间
在区间![]() 上为减函数,∴
上为减函数,∴![]() 在区间
在区间![]() 上恒成立,
上恒成立,
即![]() 在区间
在区间![]() 上恒成立,
上恒成立,
∴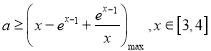 ,设
,设![]()
则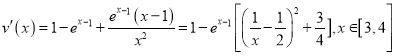 ,
,
∵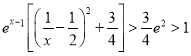 ,
,
∴![]() ,则
,则![]() 在区间
在区间![]() 上为减函数,
上为减函数,
∴![]() 在区间
在区间![]() 上的最大值
上的最大值![]() ,∴
,∴![]() ,
,
试题解析:(1)由题得, ![]() ,
,
令![]() ,得
,得![]() .,
.,
列表如下:
|
| 1 |
|
| 大于0 | 0 | 小于0 |
|
| 极大值 |
|
∴当![]() 时,
时, ![]() 取得极大值
取得极大值![]() ,无极小值;
,无极小值;
(2)当![]() 时,
时, ![]() ,
,
∵![]() 在区间
在区间![]() 上恒成立,
上恒成立,
∴![]() 在区间
在区间![]() 上为增函数,
上为增函数,
设![]() ,
,
∵![]() 在区间
在区间![]() 上恒成立,
上恒成立,
∴![]() 在区间
在区间![]() 上为增函数,不妨设
上为增函数,不妨设![]() ,
,
则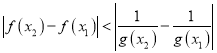 等价于
等价于![]() ,
,
即![]() ,
,
设![]() ,
,
则![]() 在区间
在区间![]() 上为减函数,
上为减函数,
∴![]() 在区间
在区间![]() 上恒成立,
上恒成立,
∴![]() 在区间
在区间![]() 上恒成立,
上恒成立,
∴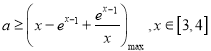 ,
,
设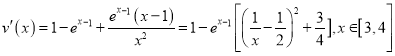 ,
,
∵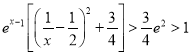 ,
,
∴![]() ,则
,则![]() 在区间
在区间![]() 上为减函数,
上为减函数,
∴![]() 在区间
在区间![]() 上的最大值
上的最大值![]() ,∴
,∴![]() ,
,
∴实数![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
相关题目
【题目】某学校为了调查喜欢语文学科与性别的关系,随机调查了一些学生情况,具体数据如下表:
调查统计 | 不喜欢语文 | 喜欢语文 |
男 | 13 | 10 |
女 | 7 | 20 |
为了判断喜欢语文学科是否与性别有关系,根据表中的数据,得到K2的观测值
k=![]() ≈4.844,因为k≥3.841,根据下表中的参考数据:
≈4.844,因为k≥3.841,根据下表中的参考数据:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
判定喜欢语文学科与性别有关系,那么这种判断出错的可能性为( )
A. 95% B. 50% C. 25% D. 5%