题目内容
过点(-1,6)与圆x +y
+y +6x-4y+9=0相切的直线方程是________.
+6x-4y+9=0相切的直线方程是________.
3x-4y+27=0或x=-1.
解析试题分析:圆x +y
+y +6x-4y+9=0,即
+6x-4y+9=0,即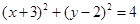 。点(-1,6)在圆x
。点(-1,6)在圆x +y
+y +6x-4y+9=0外,所以,过点(-1,6)与圆x
+6x-4y+9=0外,所以,过点(-1,6)与圆x +y
+y +6x-4y+9=0相切的直线有两条。
+6x-4y+9=0相切的直线有两条。
当切线的斜率不存在时,x=-1符合题意;
当切线的斜率存在时,设切线方程为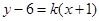 ,即
,即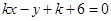 。
。
由圆心(-3,2)到切线距离等于半径2,得,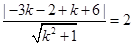 ,解得,k=
,解得,k=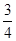 ,
,
所以,切线方程为3x-4y+27=0。
综上知,答案为3x-4y+27=0或x=-1.
考点:直线与圆的位置关系
点评:中档题,研究直线与圆的位置关系问题,利用“代数法”,须研究方程组解的情况;利用“几何法”,则要研究圆心到直线的距离与半径比较。本题易错,忽视斜率不存在的情况。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的渐近线与圆
的渐近线与圆 有公共点,则该双曲线离心率的取值范围是__________.
有公共点,则该双曲线离心率的取值范围是__________. ,
,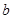 随机取自集合
随机取自集合 ,则直线
,则直线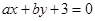 与圆
与圆 有公共点的概率是
有公共点的概率是 与圆
与圆 相交于两点
相交于两点 ,若
,若 ,则
,则 (O为坐标原点)等于________.
(O为坐标原点)等于________. 上一动点,则A到直线
上一动点,则A到直线 的最大距离为______.
的最大距离为______. ,当竹竿滑动到A1B1位置时,
,当竹竿滑动到A1B1位置时, ,竹竿在滑动时中点T也沿着某种轨迹运动到T1点,则T运动的路程是_________米.
,竹竿在滑动时中点T也沿着某种轨迹运动到T1点,则T运动的路程是_________米.
 .则直线
.则直线 被圆
被圆
 所截得的弦长为 .
所截得的弦长为 .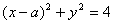 的圆心坐标为
的圆心坐标为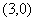 ,则实数
,则实数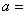 .
. 与圆
与圆 相切,则实数
相切,则实数 的值为 .
的值为 .