题目内容
已知四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AA1=2,底面四边形ABCD的边长均大于2,且∠DAB=45°,点P在底面ABCD内运动且在AB,AD上的射影分别为M,N,若|PA|=2,则三棱锥P-D1MN体积的最大值为( )
分析:画出四棱柱图形,设∠NAP=θ,求出PN,PM,得△PMN的面积,然后求出三棱锥P-D1MN的体积表达式,得最大值.
解答: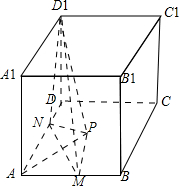 解:由题意画出四棱柱ABCD-A1B1C1D1如图:
解:由题意画出四棱柱ABCD-A1B1C1D1如图:
在底面四边形ABCD中,设∠NAP=θ,θ∈[0,45°],则∠PAM=45°-θ,
所以PN=|PA|sinθ=2sinθ,PM=|PA|sin(45°-θ)=2sin(45°-θ),
所以S△PMN=
PN•PMsin135°=
×2sinθ×2sin(45°-θ)×
=
sinθsin(45°-°θ),
∴三棱锥P-D1MN的体积为,
V三棱锥P-D1MN═
Sh=
×S△PMN×DD1=
×
sinθsin(45°-θ)×2=
×2(sinθcosθ-sin2θ)=
×(sin2θ+cos2θ-1)=
×sin(2θ+45°)-
,
因为θ∈[0,45°],所以当θ=22.5°时V三棱锥P-D1MN取得最大值为:
-
.
故选:A.
 解:由题意画出四棱柱ABCD-A1B1C1D1如图:
解:由题意画出四棱柱ABCD-A1B1C1D1如图:在底面四边形ABCD中,设∠NAP=θ,θ∈[0,45°],则∠PAM=45°-θ,
所以PN=|PA|sinθ=2sinθ,PM=|PA|sin(45°-θ)=2sin(45°-θ),
所以S△PMN=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |
∴三棱锥P-D1MN的体积为,
V三棱锥P-D1MN═
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
| 1 |
| 3 |
因为θ∈[0,45°],所以当θ=22.5°时V三棱锥P-D1MN取得最大值为:
| ||
| 3 |
| 1 |
| 3 |
故选:A.
点评:本题考查了空间中的位置关系以及锥体体积的计算问题,是基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
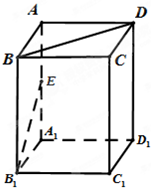 已知四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,AA1=2,E是侧棱AA1的中点,求
已知四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,AA1=2,E是侧棱AA1的中点,求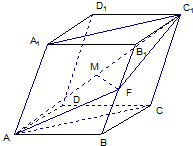 已知四棱柱ABCD-A1B1C1D1中的底面是菱形,且∠DAB=∠A1AB=∠A1AD=60°,AD=1,AA1=a,F为棱BB的中点,M为线段AC的中点.设
已知四棱柱ABCD-A1B1C1D1中的底面是菱形,且∠DAB=∠A1AB=∠A1AD=60°,AD=1,AA1=a,F为棱BB的中点,M为线段AC的中点.设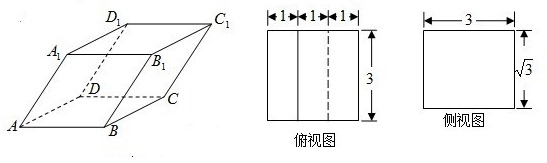 (2012•江门一模)如图,已知四棱柱ABCD-A1B1C1D1的俯视图是边长为3的正方形,侧视图是长为3宽为
(2012•江门一模)如图,已知四棱柱ABCD-A1B1C1D1的俯视图是边长为3的正方形,侧视图是长为3宽为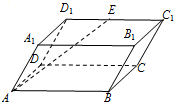 如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AA1=3,∠BAA1=60°,E为棱C1D1的中点,则
如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AA1=3,∠BAA1=60°,E为棱C1D1的中点,则