题目内容
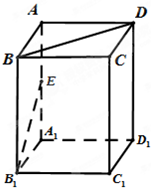 已知四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,AA1=2,E是侧棱AA1的中点,求
已知四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,AA1=2,E是侧棱AA1的中点,求(1)求异面直线BD与B1E所成角的大小;
(2)求四面体AB1D1C的体积.
分析:(1)连接B1D1、D1E,可得平行四边形BB1D1D中,B1D1∥BD,所以∠EB1D1或其补角就是异面直线BD与B1E所成角.再由已知条件算出△B1D1E是等边三角形同,从而可得异面直线BD与B1E所成角的大小为60°;
(2)算出正四棱柱ABCD-A1B1C1D1位于B、A1、C1、D四个角上的全等的三棱锥的体积,再用正四棱柱ABCD-A1B1C1D1的体积减去这四个三棱锥体积,即可得到四面体AB1D1C的体积.
(2)算出正四棱柱ABCD-A1B1C1D1位于B、A1、C1、D四个角上的全等的三棱锥的体积,再用正四棱柱ABCD-A1B1C1D1的体积减去这四个三棱锥体积,即可得到四面体AB1D1C的体积.
解答:解:(1)连接B1D1、D1E,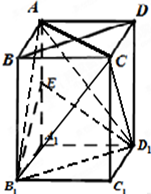
∵正四棱柱ABCD-A1B1C1D1中,B1B∥D1D且B1B=D1D
∴四边形BB1D1D是平等四边形
因此B1D1∥BD,可得∠EB1D1或其补角就是异面直线BD与B1E所成角
∵AA1=2AB=2,∴B1D1=ED1=B1E=
,得△B1D1E是等边三角形,∠EB1D1=60°
由此可得,异面直线BD与B1E所成角的大小为60°;
(2)根据题意,得V正四棱柱ABCD-A1B1C1D1=S正方形ABCD×AA1=2
∵V三棱锥B-ACB1=V三棱锥 A1-AB1D1=V三棱锥 C1-CB1D1=V三棱锥 D -AC D1=
×
×1×1×2=
∴四面体AB1D1C的体积为
V=V正四棱柱ABCD-A1B1C1D1-(V三棱锥 B -AC B1+V三棱锥 A1-AB1D1
+V三棱锥 C1-CB1D1+V三棱锥 D -AC D1)=2-
=

∵正四棱柱ABCD-A1B1C1D1中,B1B∥D1D且B1B=D1D
∴四边形BB1D1D是平等四边形
因此B1D1∥BD,可得∠EB1D1或其补角就是异面直线BD与B1E所成角
∵AA1=2AB=2,∴B1D1=ED1=B1E=
| 2 |
由此可得,异面直线BD与B1E所成角的大小为60°;
(2)根据题意,得V正四棱柱ABCD-A1B1C1D1=S正方形ABCD×AA1=2
∵V三棱锥B-ACB1=V三棱锥 A1-AB1D1=V三棱锥 C1-CB1D1=V三棱锥 D -AC D1=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
∴四面体AB1D1C的体积为
V=V正四棱柱ABCD-A1B1C1D1-(V三棱锥 B -AC B1+V三棱锥 A1-AB1D1
+V三棱锥 C1-CB1D1+V三棱锥 D -AC D1)=2-
| 4 |
| 3 |
| 2 |
| 3 |
点评:本题在正四棱柱中求异面直线所成角,并求四面体的体积,着重考查了正棱柱的性质、异面直线所成角和体积的求法等知识,属于基础题.

练习册系列答案
相关题目
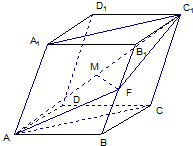 已知四棱柱ABCD-A1B1C1D1中的底面是菱形,且∠DAB=∠A1AB=∠A1AD=60°,AD=1,AA1=a,F为棱BB的中点,M为线段AC的中点.设
已知四棱柱ABCD-A1B1C1D1中的底面是菱形,且∠DAB=∠A1AB=∠A1AD=60°,AD=1,AA1=a,F为棱BB的中点,M为线段AC的中点.设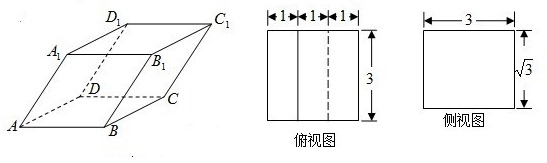 (2012•江门一模)如图,已知四棱柱ABCD-A1B1C1D1的俯视图是边长为3的正方形,侧视图是长为3宽为
(2012•江门一模)如图,已知四棱柱ABCD-A1B1C1D1的俯视图是边长为3的正方形,侧视图是长为3宽为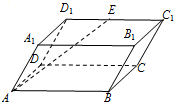 如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AA1=3,∠BAA1=60°,E为棱C1D1的中点,则
如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AA1=3,∠BAA1=60°,E为棱C1D1的中点,则