题目内容
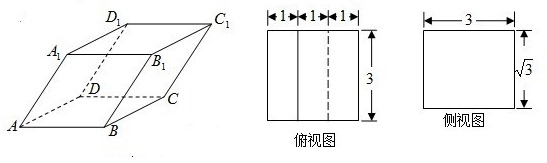 (2012•江门一模)如图,已知四棱柱ABCD-A1B1C1D1的俯视图是边长为3的正方形,侧视图是长为3宽为
(2012•江门一模)如图,已知四棱柱ABCD-A1B1C1D1的俯视图是边长为3的正方形,侧视图是长为3宽为| 3 |
(1)求该四棱柱的体积;
(2)取DD1的中点E,证明:面BCE⊥面ADD1A1.
分析:(1)可得底面ABCD是矩形,侧面ABB1A1与底面垂直,过A1作底面垂线的垂足是AB的中点,故体积V=SABCD×h,代入数据计算可得;(2)连接CD1,由△CDD1是正三角形可得CE⊥DD1,由线面垂直的性质可得AD⊥CE,可判CE⊥面ADD1A1,由面面垂直的判定可得结论.
解答:解:(1)由题意可得四棱柱的底面ABCD是矩形,侧面ABB1A1与底面垂直,
过A1作底面垂线的垂足是AB的中点,
所以四棱柱的体积V=SABCD×h=AB×AD×h
=2×3×
=6
…(6分)
(2)连接CD1,依题意△CDD1是正三角形,所以CE⊥DD1,
又AD⊥面CDD1C1,CE?面CDD1C1,所以AD⊥CE,
因为AD∩DD1=D,所以CE⊥面ADD1A1,
因为CE?面BCE,面BCE⊥面ADD1A1…(12分)
过A1作底面垂线的垂足是AB的中点,
所以四棱柱的体积V=SABCD×h=AB×AD×h
=2×3×
| 3 |
| 3 |
(2)连接CD1,依题意△CDD1是正三角形,所以CE⊥DD1,
又AD⊥面CDD1C1,CE?面CDD1C1,所以AD⊥CE,
因为AD∩DD1=D,所以CE⊥面ADD1A1,
因为CE?面BCE,面BCE⊥面ADD1A1…(12分)
点评:本题考查平面与平面垂直的判定,涉及几何体的体积的求解,属中档题.

练习册系列答案
相关题目
 (2012•江门一模)(几何证明选讲选做题)
(2012•江门一模)(几何证明选讲选做题)
 (2012•江门一模)如图,某几何体的正视图和侧视图都是对角线长分别为4和3的菱形,俯视图是对角线长为3的正方形,则该几何体的体积为( )
(2012•江门一模)如图,某几何体的正视图和侧视图都是对角线长分别为4和3的菱形,俯视图是对角线长为3的正方形,则该几何体的体积为( ) (2012•江门一模)如图,四边形ABCD中,AB=5,AD=3,cosA=
(2012•江门一模)如图,四边形ABCD中,AB=5,AD=3,cosA=