题目内容
15.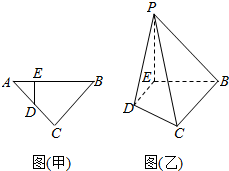 如图(甲),等腰直角三角形的底边AB=4,点D在线段AC上,DE⊥AB于点E,现将△ADE沿DE折起到△PDE的位置(如图(乙))
如图(甲),等腰直角三角形的底边AB=4,点D在线段AC上,DE⊥AB于点E,现将△ADE沿DE折起到△PDE的位置(如图(乙))(Ⅰ)求证:PB⊥DE;
(Ⅱ)若PE⊥BE,PD=$\sqrt{2}$,求四棱锥P-DEBC的体积.
分析 (I)根据翻折后DE仍然与BE、PE垂直,结合线面垂直的判定定理可得DE⊥平面PEB,再由线面垂直的性质可得PB⊥DE;
(II)证明PE⊥平面DEBC,PE是四棱锥P-DEBC的高,求出DEBC的面积,即可求四棱锥P-DEBC的体积.
解答 (Ⅰ)证明:∵DE⊥AB,∴DE⊥BE,DE⊥PE,
∵BE∩PE=E,∴DE⊥平面PEB,
又∵PB?平面PEB,∴BP⊥DE;
(Ⅱ)解:∵PE⊥BE,PE⊥DE,DE∩BE=E,
∴PE⊥平面DEBC,
∴PE是四棱锥P-DEBC的高.
在等腰直角三角形PED中,由PD=$\sqrt{2}$,可得PE=1,
∴在等腰直角三角形AED中,AE=DE=1,S△AED=$\frac{1}{2}×DE×AE$=$\frac{1}{2}$,
在等腰直角三角形ACB中,过C作CM⊥AB于M,则CM=2,
∴S△ACB=$\frac{1}{2}×AB×CM$=4,∴SDEBC=4-$\frac{1}{2}$=$\frac{7}{2}$,
∴VP-DEBC=$\frac{1}{3}×\frac{7}{2}×1$=$\frac{7}{6}$.
点评 本题考查求四棱锥P-DEBC的体积,考查线面垂直的判定与性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
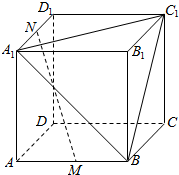 如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别为AB,A1D1的中点.
如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别为AB,A1D1的中点.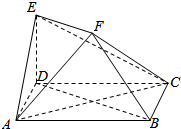 如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD.
如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD.