题目内容

10．如图所示，在棱长为1的正方体ABCD-A1B1C1D1中，M，N分别为AB，A1D1的中点．
（1）求证：MN∥平面A1BC1；
（2）求三棱锥B1-A1BC1的体积．

分析 （1）取A1C1的中点E，连接NE，BE，证明NEBM是平行四边形，可得MN∥BE，即可证明MN∥平面A1BC1；
（2）转换底面求三棱锥B1-A1BC1的体积．

解答 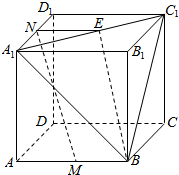（1）证明：取A1C1的中点E，连接NE，BE，则
∵M，N分别为AB，A1D1的中点，
∴NE平行且等于MB，
∴NEBM是平行四边形，
∴MN∥BE，
∵MN?平面A1BC1，BE?平面A1BC1，
∴MN∥平面A1BC1；
（2）解：三棱锥B1-A1BC1的体积=三棱锥B-A1B1C1的体积=$\frac{1}{3}×\frac{1}{2}×1×1×1$=$\frac{1}{6}$．

点评 本题考查直线与平面平行的判定，考查三棱锥B1-A1BC1的体积，考查学生分析解决问题的能力，属于中档题．

练习册系列答案
相关题目
6．已知对任意平面向量$\overrightarrow{AB}$=（x，y），把$\overrightarrow{AB}$绕其起点沿逆时针方向旋转θ角得到向量$\overrightarrow{AP}$=（xcosθ-ysinθ，xsinθ+ycosθ），叫做把点B绕点A逆时针方向旋转角得到点P．
（1）已知平面内点A（1，2），点B（1+$\sqrt{2}，2-2\sqrt{2}$）．把点B绕点A沿逆时针旋转$\frac{π}{4}$后得到点P，求点P的坐标；
（2）设平面曲线C上的每一点绕坐标原点沿逆时针方向旋转$\frac{π}{4}$后得到的点的轨迹是曲线x2-y2=3，求原来曲线C的方程．
1．在四棱锥S-ABCD中，为了推出AB⊥BC，需从下列条件：
①SB⊥面ABCD；②SC⊥CD；③CD∥面SAB；④BC⊥CD中选出部分条件，这些条件可能是（　　）
A．②③B．①④C．②④D．③④
18．已知f（x）=$\sqrt{3}$sinωx+cosωx（ω＞0），x∈R，在曲线y=f（x）与直线y=1的交点中，若相邻交点距离的最小值为$\frac{π}{3}$，则f（x）的最小正周期为π．
5．已知函数f（x）=（sinωx+cosωx）2+$\sqrt{3}$（sin2ωx-cos2ωx），（ω＞0）的最小正周期为π．
（1）求ω的值及f（x）的单调递增区间；
（2）在锐角△ABC中，角ABC所对的边分别为abc，f （A）=$\sqrt{3}$+1，a=2，且b+c=4，求△ABC的面积．
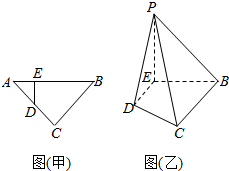15．如图（甲），等腰直角三角形的底边AB=4，点D在线段AC上，DE⊥AB于点E，现将△ADE沿DE折起到△PDE的位置（如图（乙））
（Ⅰ）求证：PB⊥DE；
（Ⅱ）若PE⊥BE，PD=$\sqrt{2}$，求四棱锥P-DEBC的体积．
2．已知函数f（x）=2$\sqrt{3}$sin$\frac{x}{2}$cos$\frac{x}{2}$-2cos2$\frac{x}{2}$．
（Ⅰ）求f（$\frac{π}{3}$）的值；
（Ⅱ）求函数f（x）的单调递减区间及对称轴方程．
19．已知向量$\overrightarrow{a}$=（$\sqrt{2}$sinx，$\frac{{\sqrt{2}}}{2}$（cosx+sinx）），$\overrightarrow{b}$=（cosx，sinx-cosx），函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$．
（Ⅰ）求y=f（x）的单调递增区间；
（Ⅱ）若将f（x）的图象向左平移$\frac{π}{4}$个单位，再将各点的纵坐标伸长为原来的2倍，横坐标不变，得到函数g（x）的图象．写出g（x）的解析式并在给定的坐标系中画出它在区间[0，π]上的图象．
20．数列{an}满足a1=1，Sn=n，则a2012=（　　）
A．1B．2010C．2011D．2012

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网