题目内容
4.已知点O为三棱锥P-ABC的顶点P在平面ABC内的投影,若PA=PB=PC,则O为△ABC的外心;若PA⊥BC,PB⊥AC,则O为△ABC的垂心;若P到三边AB,BC,CA的距离都想等且点O在△ABC的内部,则O为△ABC的内心.分析 PA=PB=PC时,得出OA=OB=OC,O为三角形的外心;
PA⊥BC,PB⊥AC时,得出AO⊥BC,BO⊥AC,O为△ABC的垂心;
P到三边AB,BC,CA的距离都相等,且点O在△ABC的内部时,得出点O到三角形三边的距离相等,是内心.
解答 解:点O为三棱锥P-ABC的顶点P在平面ABC内的投影,
当PA=PB=PC时,如图1所示: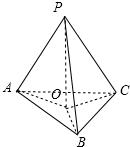
连接OA,OB,OC,
∵PA=PB=PC,
∵PO⊥底面ABC,
PO⊥OA,PO⊥OB,PO⊥OC,
∵PA=PB=PC,
∴OA=OB=OC
所以O为三角形的外心.
O为△ABC的外心;
同理,当PA⊥BC,PB⊥AC时,AO⊥BC,BO⊥AC,
所以O为△ABC的垂心;
当P到三边AB,BC,CA的距离都相等,且点O在△ABC的内部时,
得出点O到三角形三边的距离相等,
所以点O为△ABC的内心.
故答案为:外、垂、内.
点评 本题考查了三棱锥的顶点在底面三角形内的射影与三角形的四心(内心、外心、垂心和重心)问题,是基础题目.

练习册系列答案
相关题目
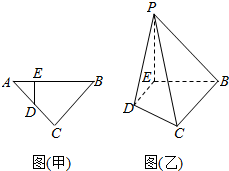 如图(甲),等腰直角三角形的底边AB=4,点D在线段AC上,DE⊥AB于点E,现将△ADE沿DE折起到△PDE的位置(如图(乙))
如图(甲),等腰直角三角形的底边AB=4,点D在线段AC上,DE⊥AB于点E,现将△ADE沿DE折起到△PDE的位置(如图(乙)) 已知向量$\overrightarrow{a}$=($\sqrt{2}$sinx,$\frac{{\sqrt{2}}}{2}$(cosx+sinx)),$\overrightarrow{b}$=(cosx,sinx-cosx),函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$.
已知向量$\overrightarrow{a}$=($\sqrt{2}$sinx,$\frac{{\sqrt{2}}}{2}$(cosx+sinx)),$\overrightarrow{b}$=(cosx,sinx-cosx),函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$.