题目内容
5.已知$y=sin(\frac{π}{6}+2x)+cos2x$(1)将函数化为正弦型函数y=Asin(ωx+φ)的形式;
(2)求函数的最小正周期及单调递增区间.
分析 (1)由条件利用三角恒等变换,化简函数的解析式.
(2)根据函数的解析式再利用正弦函数的周期性和单调性,求得函数的最小正周期及单调递增区间.
解答 解:(1)∵$y=sin(\frac{π}{6}+2x)+cos2x$=$\frac{\sqrt{3}}{2}$sin2x+$\frac{3}{2}$cos2x=$\sqrt{3}$sin(2x+$\frac{π}{3}$).
(2)根据y=$\sqrt{3}$sin(2x+$\frac{π}{3}$),求得它的最小正周期为$\frac{2π}{2}$=π.
令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{3}$,求得kπ-$\frac{5π}{12}$≤x≤kπ+$\frac{π}{12}$,
可得它的单调递增区间为:[kπ-$\frac{5π}{12}$,kπ+$\frac{π}{12}$],k∈Z.
点评 本题主要考查三角恒等变换,正弦函数的周期性和单调性,属于基础题.

练习册系列答案
相关题目
20.数列{an}满足a1=1,Sn=n,则a2012=( )
| A. | 1 | B. | 2010 | C. | 2011 | D. | 2012 |
17.一个梯形采用斜二测画法作出其直观图,则其直观图的面积是原来梯形面积的( )
| A. | $\frac{\sqrt{2}}{4}$倍 | B. | $\frac{1}{2}$倍 | C. | $\frac{\sqrt{2}}{2}$倍 | D. | $\sqrt{2}$倍 |
15.已知a>b,则下面结论正确的是( )
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | $\frac{a}{b}>1$ | C. | |a|>b | D. | ac2>bc2 |
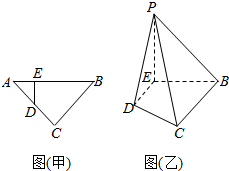 如图(甲),等腰直角三角形的底边AB=4,点D在线段AC上,DE⊥AB于点E,现将△ADE沿DE折起到△PDE的位置(如图(乙))
如图(甲),等腰直角三角形的底边AB=4,点D在线段AC上,DE⊥AB于点E,现将△ADE沿DE折起到△PDE的位置(如图(乙))