题目内容
已知函数f(x)=log2(x+m),且f(0)、f(2)、f(6)成等差数列.
(1)求实数m的值;
(2)若a、b、c是两两不相等的正数,且a、b、c成等比数列,试判断f(a)+f(c)与2f(b)的大小关系,并证明你的结论.
(1)求实数m的值;
(2)若a、b、c是两两不相等的正数,且a、b、c成等比数列,试判断f(a)+f(c)与2f(b)的大小关系,并证明你的结论.
(1)m=2.(2)f(a)+f(c)>2(b).
试题分析:(1)由f(0)、f(2)、f(6)成等差数列,
可得2log2(2+m)=log2m+log2(6+m), 3分
即(m+2)2=m(m+6),且m>0,解得m=2. 5分
(2)由f(x)=log2(x+2),
可得2f(b)=2log2(b+2)=log2(b+2)2, 6分
f(a)+f(c)=log2(a+2)+log2(c+2)=log2[(a+2)(c+2)], 7分
∵a、b、c成等比数列,∴b2=ac. 8分
又a、b、c是两两不相等的正数,
故(a+2)(c+2)-(b+2)2
=ac+2(a+c)+4-(b2+4b+4) 10分
=2(a+c-2
 )=2
)=2 >0, 12分
>0, 12分∴log2[(a+2)(c+2)]>log2(b+2)2. 13分
即f(a)+f(c)>2(b)
点评:对于此类问题除了要求学生掌握等差(等比)数列的性质之外,还有灵活运用作差法判断大小

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
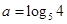 ,
, ,
, ,则( )
,则( )



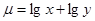 的最大值。
的最大值。 ,
, ,
, (其中
(其中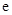 为自然对数的底数),则
为自然对数的底数),则


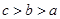
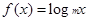 (
(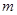 为常数,
为常数,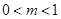 ),且数列
),且数列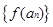 是首项为
是首项为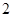 ,公差为
,公差为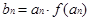 ,当
,当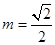 时,求数列
时,求数列 的前
的前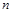 项和
项和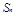 ;
; 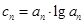 ,如果
,如果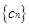 中的每一项恒小于它后面的项,求
中的每一项恒小于它后面的项,求 在
在 上为增函数,则实数a的取值范围为___________;
上为增函数,则实数a的取值范围为___________; .
.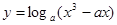 (
(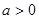 且
且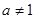 )在
)在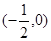 内单调递增,则
内单调递增,则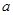 的范围是
的范围是

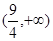

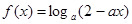 在
在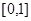 上为减函数,则
上为减函数,则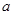 的取值范围为( )。
的取值范围为( )。