题目内容
已知: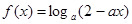 在
在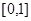 上为减函数,则
上为减函数,则 的取值范围为( )。
的取值范围为( )。
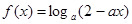 在
在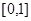 上为减函数,则
上为减函数,则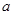 的取值范围为( )。
的取值范围为( )。A. | B. | C. | D.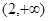 |
C
试题分析:因为
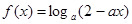 ,所以令
,所以令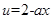 ,则
,则 ,
,当0<a<1,时,
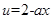 是单调递减的,
是单调递减的, 是单调递减的,所以
是单调递减的,所以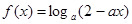 是单调递增的,此时不满足题意;
是单调递增的,此时不满足题意;当a>1时,
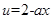 是单调递减的,
是单调递减的, 是单调递增的,所以
是单调递增的,所以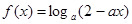 是单调递减的,又由
是单调递减的,又由 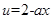 >0得
>0得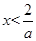 ,所以
,所以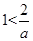 ,即
,即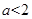 ,所以
,所以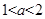 。
。综上知:a的范围为
 。
。点评:此题考查的是复合函数单调性的判断。对于复合函数的判断我们只需要掌握四个字:同增异减。同时,本题也是一个易错题,错误的主要原因为忽略了定义域的限制。因为

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
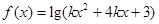 的定义域是R,则非零实数
的定义域是R,则非零实数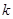 的取值范围是 。
的取值范围是 。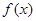 =
=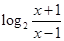 .
.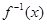 ,并求使得函数
,并求使得函数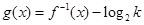 有零点的实数
有零点的实数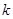 的取值范围.
的取值范围.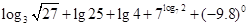 = .
= . 在[0,1]上是
在[0,1]上是 的减函数,则
的减函数,则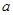 的取值范围是
的取值范围是 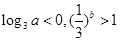 ,则( )
,则( )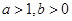
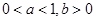
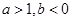
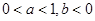
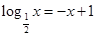 的根的个数是( )
的根的个数是( ) ,则函数
,则函数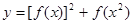 的最大值是____.
的最大值是____.