题目内容
将某个圆锥沿着母线和底面圆周剪开后展开,所得的平面图是一个圆和扇形,己知该扇形的半径为24cm,圆心角为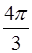 ,则圆锥的体积是________
,则圆锥的体积是________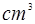 .
.
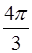 ,则圆锥的体积是________
,则圆锥的体积是________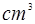 .
.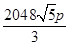
试题分析:本题考查圆锥的侧面展开图问题,我们知道圆锥侧面展开图的半径就是圆锥的母线,扇形的弧长就是圆锥底面周长,因此有
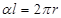 ,故
,故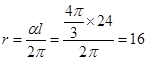 ,那么圆锥的高为
,那么圆锥的高为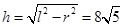 ,所以体积为
,所以体积为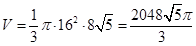 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
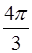 ,则圆锥的体积是________
,则圆锥的体积是________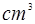 .
.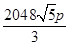
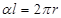 ,故
,故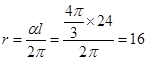 ,那么圆锥的高为
,那么圆锥的高为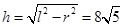 ,所以体积为
,所以体积为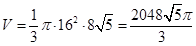 .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案