题目内容
【题目】如图，在平行四边形OABC中，点C（1，3）．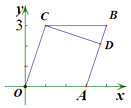 
（1）求OC所在直线的斜率；
（2）过点C作CD⊥AB于点D，求CD所在直线的方程．
【答案】
（1）解：∵点O（0，0），点C（1，3），
∴OC所在直线的斜率为 
（2）解：在平行四边形OABC中，AB∥OC，
∵CD⊥AB，
∴CD⊥OC．∴CD所在直线的斜率为 
．
∴CD所在直线方程为 
，即x+3y﹣10=0
【解析】（1）根据原点坐标和已知的C点坐标，利用直线的斜率k= 
，求出直线OC的斜率即可；（2）根据平行四边形的两条对边平行得到AB平行于OC，又CD垂直与AB，所以CD垂直与OC，由（1）求出的直线OC的斜率，根据两直线垂直时斜率乘积为﹣1，求出CD所在直线的斜率，然后根据求出的斜率和点C的坐标写出直线CD的方程即可．
【考点精析】掌握斜率的计算公式和点斜式方程是解答本题的根本，需要知道给定两点P1(x1,y1),P2(x2,y2),x1≠x2,用两点的坐标来表示直线P1P2的斜率：斜率公式: k=y2-y1/x2-x1；直线的点斜式方程：直线
经过点
，且斜率为
则：
．
练习册系列答案
相关题目
