题目内容
【题目】已知椭圆C： 
=1（a＞b＞0）的左、右焦点分别为F1 ， F2 ， 且F1 ， F2与短轴的一个顶点Q构成一个等腰直角三角形，点P（ 
， 
）在椭圆C上．
（I）求椭圆C的标准方程；
（Ⅱ）过F2作互相垂直的两直线AB，CD分别交椭圆于点A，B，C，D，且M，N分别是弦AB，CD的中点，求△MNF2面积的最大值．
【答案】解：（Ⅰ）∵椭圆 
=1（a＞b＞0）经过点P（ 
， 
），
且F1 ， F2与短轴的一个顶点Q构成一个等腰直角三角形，
∴ 
，解得a2=2，b2=1，
∴椭圆方程为 
；
（Ⅱ）设直线AB的方程为x=my+1，m≠0，
则直线CD的方程为x=﹣ 
y+1，
联立 
，消去x得（m2+2）y2+2my﹣1=0，
设A（x1 ， y1），B（x2 ， y2），则y1+y2=﹣ 
，y1y2= 
，
∴x1+x2=（my1+1）+（my2+1）
=m（y1+y2）+2= 
，
由中点坐标公式得M（ 
），
将M的坐标中的m用﹣ 代换，得CD的中点N（ 
），
kMN= 
，
直线MN的方程为y+ 
= （x﹣ 
），
即为y= 
，
令 
，可得x= 
，即有y=0，
则直线MN过定点H，且为H（ ，0），
∴△F2MN面积为S= 
|F2H||yM﹣yN|
= （1﹣ ）| 
|= | 
|= | 
|，
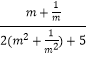令m+ =t（t≥2），由于2t+ 
的导数为2﹣ 
，且大于0，即有在[2，+∞）递增．
即有S= 
= 
在[2，+∞）递减，
∴当t=2，即m=1时，S取得最大值，为 
；
则△MNF2面积的最大值为
【解析】（Ⅰ）由已知得到关于a，b，c的方程组，求解方程组可得a，b，进而得到椭圆方程；（Ⅱ）设直线AB的方程为x=my+1，m≠0，则直线CD的方程为x=﹣ y+1，分别代入椭圆方程，由于韦达定理和中点坐标公式可得中点M，N的坐标，求得斜率和直线方程，即可得到定点H，则△MNF2面积为S= |F2H||yM﹣yN|，化简整理，再令m+ =t（t≥2），由于函数的单调性，即可得到最大值．
