题目内容
已知动点P与双曲线 的两个焦点F1、F2的距离之和为6.
的两个焦点F1、F2的距离之和为6.(1)求动点P的轨迹C的方程;
(2)
 •
• ,求△PF1F2的面积;
,求△PF1F2的面积;(3)若已知D(0,3),M、N在曲线C上,且
 ,求实数λ的取值范围.
,求实数λ的取值范围.
【答案】分析:(1)先求出焦点坐标,根据动点P到两个焦点F1,F2的距离之和为定值6且6>2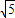 ,可得动点P的运动轨迹是以F1、F2为焦点的椭圆;再求出对应的a,b,c即可找到动点P的轨迹C的方程;
,可得动点P的运动轨迹是以F1、F2为焦点的椭圆;再求出对应的a,b,c即可找到动点P的轨迹C的方程;
(2)先设出点P的坐标,代入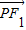 •
•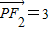 ,得到关于点P的坐标的一个方程;再结合点P的轨迹C的方程可求出点P的纵坐标的绝对值;最后代入三角形的面积计算公式即可;
,得到关于点P的坐标的一个方程;再结合点P的轨迹C的方程可求出点P的纵坐标的绝对值;最后代入三角形的面积计算公式即可;
(3)设出直线MN的方程以及点M,N的坐标,联立直线方程与曲线C的对应方程,根据两者有公共点,可以求出k的取值范围以及点M,N的坐标与k的关系;再结合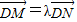 ,求出点M,N的坐标与λ的之间的关系;最后通过消去M,N的坐标来求实数λ的取值范围.
,求出点M,N的坐标与λ的之间的关系;最后通过消去M,N的坐标来求实数λ的取值范围.
解答:解:(1)由双曲线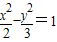 的两个焦点:F1、F2.
的两个焦点:F1、F2.
可知F1(-√5,0),F2(√5,0)
∵动点P到两个焦点F1,F2的距离之和为定值6且6>2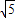
∴动点P的运动轨迹是以F1、F2为焦点的椭圆
∴c=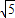 ,a=3,b2=a2-c2=4.
,a=3,b2=a2-c2=4.
∴动点P的轨迹C的方程: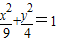 .
.
(2)设P(x,y),则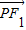 =(
=(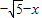 ,-y);
,-y);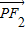 =(
=(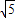 -x,-y);
-x,-y);
∴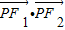 =x2-5+y2=3.
=x2-5+y2=3.
∵点P的轨迹C的方程: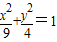 .
.
∴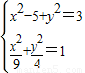 ⇒y2=
⇒y2= ⇒
⇒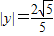 .
.
∴S△= |F1F2|•|y|=
|F1F2|•|y|= ×2
×2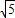 ×
×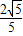 =2.
=2.
(3)设M(x1,y1),N(x2,y2),
把直线MN的方程为y=kx+3代入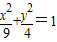 消去x整理得
消去x整理得
:(4+9k2)x2+54kx+45=0
∵△=54×54k2-4×45(4+9k2)≥0
∴k2≥ …①
…①
∴x1+x2=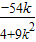 …②,
…②,
x1•x2=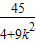 …③
…③
∵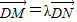 ,
,
∴x1=λx2…④
由②③④并消去x1与x2…并整理得: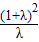 =
=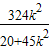
再由①可得4≤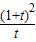 <
<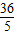
解得 ≤t≤5
≤t≤5
当k不存在时此时MN为短轴容易得t= 或5
或5
综上可知λ取值范围为[ ,5]
,5]
点评:本题综合考查了直线与椭圆的位置关系以及向量共线问题.直线与圆锥曲线的位置关系,由于集中交汇了直线,圆锥曲线两章的知识内容,综合性强,能力要求高,还涉及到函数,方程,不等式,平面几何等许多知识,可以有效的考查函数与方程的思想,数形结合的思想,分类讨论的思想和转化化归的思想,因此,这一部分内容也成了高考的热点和重点,一般是以压轴题的形式出现.
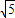 ,可得动点P的运动轨迹是以F1、F2为焦点的椭圆;再求出对应的a,b,c即可找到动点P的轨迹C的方程;
,可得动点P的运动轨迹是以F1、F2为焦点的椭圆;再求出对应的a,b,c即可找到动点P的轨迹C的方程;(2)先设出点P的坐标,代入
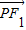 •
•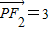 ,得到关于点P的坐标的一个方程;再结合点P的轨迹C的方程可求出点P的纵坐标的绝对值;最后代入三角形的面积计算公式即可;
,得到关于点P的坐标的一个方程;再结合点P的轨迹C的方程可求出点P的纵坐标的绝对值;最后代入三角形的面积计算公式即可;(3)设出直线MN的方程以及点M,N的坐标,联立直线方程与曲线C的对应方程,根据两者有公共点,可以求出k的取值范围以及点M,N的坐标与k的关系;再结合
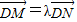 ,求出点M,N的坐标与λ的之间的关系;最后通过消去M,N的坐标来求实数λ的取值范围.
,求出点M,N的坐标与λ的之间的关系;最后通过消去M,N的坐标来求实数λ的取值范围.解答:解:(1)由双曲线
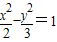 的两个焦点:F1、F2.
的两个焦点:F1、F2.可知F1(-√5,0),F2(√5,0)
∵动点P到两个焦点F1,F2的距离之和为定值6且6>2
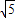
∴动点P的运动轨迹是以F1、F2为焦点的椭圆
∴c=
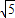 ,a=3,b2=a2-c2=4.
,a=3,b2=a2-c2=4.∴动点P的轨迹C的方程:
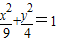 .
.(2)设P(x,y),则
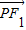 =(
=(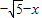 ,-y);
,-y);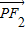 =(
=(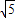 -x,-y);
-x,-y);∴
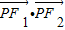 =x2-5+y2=3.
=x2-5+y2=3.∵点P的轨迹C的方程:
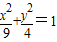 .
.∴
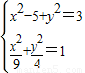 ⇒y2=
⇒y2= ⇒
⇒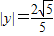 .
.∴S△=
 |F1F2|•|y|=
|F1F2|•|y|= ×2
×2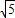 ×
×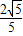 =2.
=2.(3)设M(x1,y1),N(x2,y2),
把直线MN的方程为y=kx+3代入
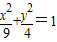 消去x整理得
消去x整理得:(4+9k2)x2+54kx+45=0
∵△=54×54k2-4×45(4+9k2)≥0
∴k2≥
 …①
…①∴x1+x2=
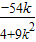 …②,
…②,x1•x2=
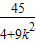 …③
…③∵
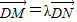 ,
,∴x1=λx2…④
由②③④并消去x1与x2…并整理得:
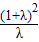 =
=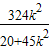
再由①可得4≤
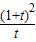 <
<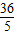
解得
 ≤t≤5
≤t≤5当k不存在时此时MN为短轴容易得t=
 或5
或5综上可知λ取值范围为[
 ,5]
,5]点评:本题综合考查了直线与椭圆的位置关系以及向量共线问题.直线与圆锥曲线的位置关系,由于集中交汇了直线,圆锥曲线两章的知识内容,综合性强,能力要求高,还涉及到函数,方程,不等式,平面几何等许多知识,可以有效的考查函数与方程的思想,数形结合的思想,分类讨论的思想和转化化归的思想,因此,这一部分内容也成了高考的热点和重点,一般是以压轴题的形式出现.

练习册系列答案
相关题目
 的两个焦点F1,F2的距离之和为4.
的两个焦点F1,F2的距离之和为4. 的两个焦点F1,F2的距离之和为定值,
的两个焦点F1,F2的距离之和为定值, .
. 平分?若存在,求出直线l的斜率k的取值范围,若不存在说明理由.
平分?若存在,求出直线l的斜率k的取值范围,若不存在说明理由.