题目内容
已知函数f(x)=x2+2(a-1)x+2在区间(-∞,4)上是减函数,则a的取值范围是( )
| A.a>-3 | B.a<-3 | C.a≥-3 | D.a≤-3 |
D
解析试题分析:函数f(x)的对称轴为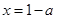 ,因为函数f(x)=x2+2(a-1)x+2在区间(-∞,4)上是减函数,所以
,因为函数f(x)=x2+2(a-1)x+2在区间(-∞,4)上是减函数,所以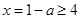 ,解得a≤-3
,解得a≤-3
考点:函数的单调性
点评:本题的函数是二次函数,其对称轴两边的单调性不一致,由于此函数的开口向上,故对称轴左边为减函数,右边为增函数。

练习册系列答案
相关题目
下列各组函数是同一函数的是
① 与
与 ;②
;② 与
与 ;③
;③ 与
与 ;④
;④ 与
与 。
。
| A.①② | B.①③ | C.②③④ | D.①④ |
若函数f(x) (x∈R)是奇函数,函数g(x) (x∈R)是偶函数,则
| A.函数f[g(x)]是奇函数 | B.函数g[f(x)]是奇函数 |
| C.函数f(x) g(x)是奇函数 | D.函数f(x)+g(x)是奇函数 |
下列函数中,在区间 上为增函数的是( ).
上为增函数的是( ).
A.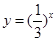 | B.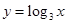 | C.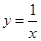 | D.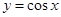 |
函数 的定义域是( )
的定义域是( )
A. | B. | C. | D. |
 为定义域和值域的函数的图像是( )
为定义域和值域的函数的图像是( )
 ,如果存在锐角
,如果存在锐角 使得
使得 的旋转性的是
的旋转性的是


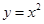

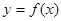 的图象如右下图所示, 则函数
的图象如右下图所示, 则函数 的图象大致为( )
的图象大致为( )
