题目内容
对于函数 ,如果存在锐角
,如果存在锐角 使得
使得 的图象绕坐标原点逆时针旋转角
的图象绕坐标原点逆时针旋转角 ,所得曲线仍是一函数,则称函数
,所得曲线仍是一函数,则称函数 具备角
具备角 的旋转性,下列函数具有角
的旋转性,下列函数具有角 的旋转性的是
的旋转性的是
A. | B. | C. | D.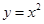 |
C
解析试题分析:若函数f(x)逆时针旋转 角后所得曲线仍是一函数,
角后所得曲线仍是一函数,
则函数f(x)的图象与任一斜率为1的直线y=x+b均不能有两个以上的交点
A中函数 与直线y=x有两个交点,不满足要求;
与直线y=x有两个交点,不满足要求;
B中函数y=lnx与直线y=x-1有两个交点,不满足要求;
C中函数 与直线y=x+b均有且只有一个交点,满足要求;
与直线y=x+b均有且只有一个交点,满足要求;
D中函数y=x2与直线y=x有两个交点,不满足要求;故选C.
考点:旋转变换
点评:本题考查的知识点是函数的定义,其中根据函数的定义分析出函数f(x)的图象与任一斜率为1的直线y=x+b均不能有两个以上的交点,是解答本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
定义在R上的函数 既是奇函数又是周期函数,若
既是奇函数又是周期函数,若 的最小正周期是
的最小正周期是 ,且当
,且当 时,
时, ,则
,则 的值为
的值为
A. | B.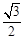 | C. | D. |
已知函数 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,不等式
时,不等式 成立,若
成立,若 ,
, ,
, ,则a,b,c间的大小关系是( ).
,则a,b,c间的大小关系是( ).
| A.a>b>c | B.c>b>a | C.c>a>b | D.a>c>b |
设 是方程
是方程 的解,则
的解,则 属于区间 ( )
属于区间 ( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
现有四个函数:① ②
② ③
③ ④
④ 的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是
的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是
| A.④①②③ | B.①④③② | C.①④②③ | D.③④②① |
已知函数f(x)=x2+2(a-1)x+2在区间(-∞,4)上是减函数,则a的取值范围是( )
| A.a>-3 | B.a<-3 | C.a≥-3 | D.a≤-3 |
设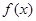 是定义域为
是定义域为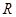 ,最小正周期为
,最小正周期为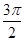 的函数。若
的函数。若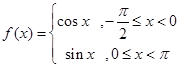 , 则
, 则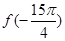 等于( )
等于( )
| A.1 | B.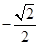 | C.0 | D.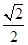 |

 的图象的大致形状是
的图象的大致形状是