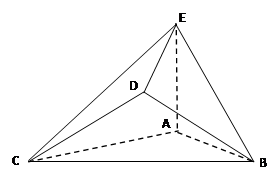题目内容
已知长方体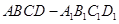 中,底面
中,底面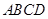 为正方形,
为正方形,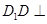 面
面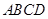 ,
, ,
,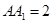 ,点
,点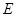 在棱
在棱 上,且
上,且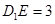 .
.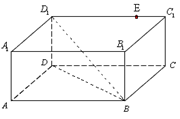
(Ⅰ)试在棱 上确定一点
上确定一点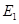 ,使得直线
,使得直线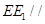 平面
平面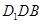 ,并证明;
,并证明;
(Ⅱ)若动点 在底面
在底面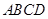 内,且
内,且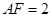 ,请说明点
,请说明点 的轨迹,并探求
的轨迹,并探求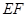 长度的最小值.
长度的最小值.
(Ⅰ)详见解析;(Ⅱ)点 在平面
在平面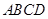 内的轨迹是以
内的轨迹是以 为圆心,半径等于2的四分之一圆弧,且
为圆心,半径等于2的四分之一圆弧,且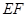 长度的最小值为
长度的最小值为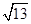 .
.
解析试题分析:(Ⅰ)先利用证明四边形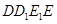 为平行四边形证明
为平行四边形证明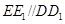 从而证明直线
从而证明直线 平面
平面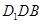 ,或者可以以
,或者可以以 平面
平面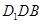 为已知条件出发,利用直线与平面平行的性质定理得到
为已知条件出发,利用直线与平面平行的性质定理得到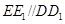 ,进而确定点
,进而确定点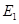 的位置;(Ⅱ)先确定四边形
的位置;(Ⅱ)先确定四边形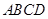 的形状以及各边的长度,然后再根据
的形状以及各边的长度,然后再根据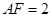 以及点
以及点 为定点这一条件确定点
为定点这一条件确定点 的轨迹,在计算
的轨迹,在计算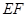 的过程中,可以利用
的过程中,可以利用 平面
平面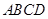 以及
以及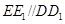 从而得到
从而得到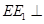 平面
平面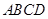 ,于是得到
,于是得到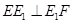 ,进而可以由勾股定理
,进而可以由勾股定理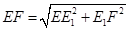 ,从而将问题转化为当
,从而将问题转化为当 取到最小值时,
取到最小值时,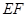 取到最小值.
取到最小值.
试题解析:(Ⅰ)取 的四等分点
的四等分点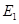 ,使得
,使得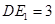 ,则有
,则有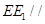 平面
平面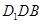 . 证明如下: 1分
. 证明如下: 1分
因为 且
且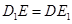 ,
,
所以四边形 为平行四边形,则
为平行四边形,则 , 2分
, 2分
因为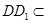 平面
平面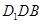 ,
,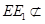 平面
平面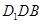 ,所以
,所以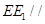 平面
平面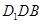 . 4分
. 4分
(Ⅱ)因为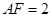 ,所以点
,所以点 在平面
在平面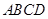 内的轨迹是以
内的轨迹是以 为圆心,半径等于2的四分之一圆弧. 6分
为圆心,半径等于2的四分之一圆弧. 6分
因为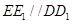 ,
,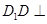 面
面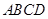 ,所以
,所以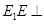 面
面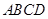 , 7分
, 7分
故 . 8分
. 8分
所以当 的长度取最小值时,
的长度取最小值时,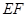 的长度最小,此时点
的长度最小,此时点 为线段
为线段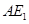 和四分之一圆弧的交点, 10分
和四分之一圆弧的交点, 10分
即 ,
,
所以 .
.
即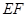 长度的最小值为
长度的最小值为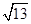 . 12分
. 12分
考点:直线与平面平行、勾股定理、点到圆上一点距离的最值

练习册系列答案
相关题目
 ,
, 是
是 边上的中点(如图甲),
边上的中点(如图甲), ,
, ,
, ,将
,将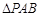 沿
沿 折到
折到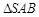 的位置,使
的位置,使 ,点
,点 在
在 上,且
上,且 (如图乙)
(如图乙)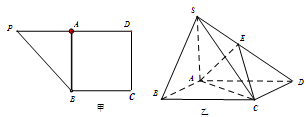
 平面ABCD.
平面ABCD.  中,底面
中,底面 为菱形,
为菱形, ,
, 为
为 的中点。
的中点。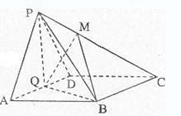
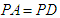 ,求证:平面
,求证:平面 ;
;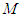 在线段
在线段 上,
上,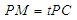 ,试确定
,试确定 的值,使
的值,使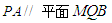 ;
; ,曲线
,曲线 在
在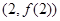 处的切线过点
处的切线过点 .
. 的解析式;
的解析式;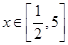 时,求
时,求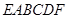 的底面
的底面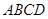 是边长为
是边长为 的正方形,
的正方形,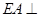 底面
底面 ,且
,且 .
. 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
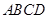 中,
中,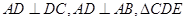 是边长为2的等边三角形,
是边长为2的等边三角形,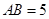 .沿
.沿 将
将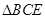 折起,使
折起,使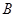 至
至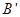 处,且
处,且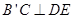 ;然后再将
;然后再将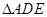 沿
沿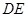 折起,使
折起,使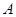 至
至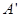 处,且面
处,且面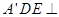 面
面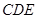 ,
,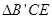 和
和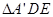 在面
在面

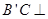 平面
平面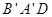 与平面
与平面 中,
中,
 为
为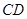 的中点,沿
的中点,沿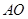 将三角形
将三角形 折起,使
折起,使 .
. ;
;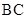 与平面
与平面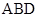 所成角的正弦值.
所成角的正弦值.
 中,
中,  是
是 上的点且
上的点且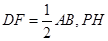 为
为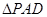 中
中 边上的高.
边上的高. 平面
平面 ;
;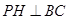 ;
; 上是否存在点
上是否存在点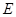 ,使
,使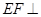 平面
平面 ?说明理由.
?说明理由.
 是边长为2的正三角形,
是边长为2的正三角形,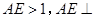 平面ABC,平面
平面ABC,平面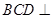 平面ABC,BD=CD,且
平面ABC,BD=CD,且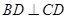 .
.