题目内容
给出以下四个命题：①已知命题p：?x∈R，tanx=2；命题q：?x∈R，x2-x+1≥0．命题p和q都是真命题；
②过点（-1，2）且在x轴和y轴上的截距相等的直线方程是x+y-1=0或2x+y=0；
③函数f（x）=lnx+2x-1在定义域内有且只有一个零点；
④先将函数
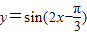的图象向左平移
个单位，再将新函数的周期扩大为原来的两倍，则所得图象的函数解析式为y=sinx．
其中正确命题的序号为 ．（把你认为正确的命题序号都填上）
【答案】分析：①命题p：?x∈R，tanx=2为真命题，命题q：x2-x+1=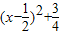
≥0成立
②过点（-1，2）且在x轴和y轴上的截距相等，分（i）当截距a=b=0（ii）当截距a=b≠0分别求解直线方程
③只需判断函数y=-2x+1的图象与函数y=lnx的图象的交点的个数即可
④根据函数的图象的平移法则及周期变化的法则可求
解答：解：①命题p：?x∈R，tanx=2为真命题，命题q：?x∈R，x2-x+1=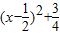
≥0为真命题，①正确
②过点（-1，2）且在x轴和y轴上的截距相等
（i）当截距a=b=0时，直线方程为y=-2x即2x+y=0
（ii）当截距a=b≠0时，可设直线方程为
，由直线过（-1，2）可得a=1，则直线方程为x+y-1=0，②正确
③根据函数的图象可知，函数y=lnz与函数y=-2x+1的函图象只有一个交点，即函数f（x）=lnx+2x-1在定义域内有且只有一个零点；③正确
④将函数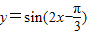
的图象向左平移
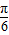个单位可得函数y=sin2x的图象，再将新函数的周期扩大为原来的两倍，可得图象的函数解析式为y=sinx．④正确
故答案为：①②③④
点评：本题主要考查了命题真假的判断，解答本题的关键是熟练掌握基本知识并能灵活应用．
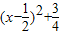≥0成立②过点（-1，2）且在x轴和y轴上的截距相等，分（i）当截距a=b=0（ii）当截距a=b≠0分别求解直线方程
③只需判断函数y=-2x+1的图象与函数y=lnx的图象的交点的个数即可
④根据函数的图象的平移法则及周期变化的法则可求
解答：解：①命题p：?x∈R，tanx=2为真命题，命题q：?x∈R，x2-x+1=
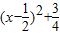≥0为真命题，①正确②过点（-1，2）且在x轴和y轴上的截距相等
（i）当截距a=b=0时，直线方程为y=-2x即2x+y=0
（ii）当截距a=b≠0时，可设直线方程为
，由直线过（-1，2）可得a=1，则直线方程为x+y-1=0，②正确③根据函数的图象可知，函数y=lnz与函数y=-2x+1的函图象只有一个交点，即函数f（x）=lnx+2x-1在定义域内有且只有一个零点；③正确
④将函数
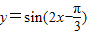的图象向左平移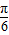个单位可得函数y=sin2x的图象，再将新函数的周期扩大为原来的两倍，可得图象的函数解析式为y=sinx．④正确故答案为：①②③④
点评：本题主要考查了命题真假的判断，解答本题的关键是熟练掌握基本知识并能灵活应用．
练习册系列答案
相关题目
定义平面向量之间的一种运算“*”如下：对任意的
=(m，n)，
=(p，q)，令
*
=mq-np．给出以下四个命题：（1）若
与
共线，则
*
=0；（2）
*
=
*
；（3）对任意的λ∈R，有(λ
)*
=λ(
*
)（4）(
*
)2+(
•
)2=|
|2•|
|2．（注：这里
•
指
与
的数量积）则其中所有真命题的序号是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、（1）（2）（3） |
| B、（2）（3）（4） |
| C、（1）（3）（4） |
| D、（1）（2）（4） |
如图所示，正方体ABCD-A′B′C′D′的棱长为1，E、F分别是棱AA′，CC′的中点，过直线EF的平面分别与棱BB′、DD′交于M、N，设BM=x，x∈[0，1]，给出以下四个命题：