题目内容
若整数m满足不等式x-
≤m<x+
,x∈R,则称m为x的“亲密整数”,记作{x},即{x}=m,已知函数f(x)x-{x}.给出以下四个命题:
①函数y=f(x),x∈R是周期函数且其最小正周期为1;
②函数y=f(x),x∈R的图象关于点(k,0),k∈Z中心对称;
③函数y=f(x),x∈R在[-
,
]上单调递增;
④方程f(x)=
sin(π•x)在[-2,2]上共有7个不相等的实数根.
其中正确命题的序号是
| 1 |
| 2 |
| 1 |
| 2 |
①函数y=f(x),x∈R是周期函数且其最小正周期为1;
②函数y=f(x),x∈R的图象关于点(k,0),k∈Z中心对称;
③函数y=f(x),x∈R在[-
| 1 |
| 2 |
| 1 |
| 2 |
④方程f(x)=
| 1 |
| 2 |
其中正确命题的序号是
①④
①④
.(写出所有正确命题的序号).分析:先通过归纳得出:{x}=m表示对x进行四舍五入后的整数,再在同一坐标系里作出函数f(x)=x-{x}和y=
sin(π•x),x结合图象讨论四个命题的正确与否,由此可得本题的正确答案.
| 1 |
| 2 |
解答:解:当-
<x≤
时,满足不等式x-
≤m<x+
,x∈R的“亲密整数”m=0,
当
<x≤
时,满足不等式x-
≤m<x+
,x∈R的“亲密整数”m=1,…,
归纳得出:{x}=m表示对x进行四舍五入后的整数,
从而作出函数f(x)=x-{x}的图象,是一些左开右闭的线段组成.如图,
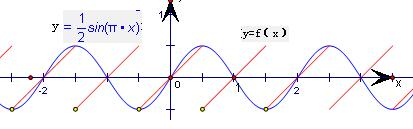
由图象可得:
①函数y=f(x),x∈R是周期函数且其最小正周期为1;正确;
②函数y=f(x),x∈R的图象不关于点(k,0),k∈Z中心对称;不正确;
③函数y=f(x),x∈R在[-
,
]上不是单调递增,因f(-
)=1,f(
)=1;故③错误;
④方程f(x)=
sin(π•x)在[-2,2]上共有7个不相等的实数根,正确.
其中正确命题的序号是 ①④.
故答案为:①④.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
归纳得出:{x}=m表示对x进行四舍五入后的整数,
从而作出函数f(x)=x-{x}的图象,是一些左开右闭的线段组成.如图,

由图象可得:
①函数y=f(x),x∈R是周期函数且其最小正周期为1;正确;
②函数y=f(x),x∈R的图象不关于点(k,0),k∈Z中心对称;不正确;
③函数y=f(x),x∈R在[-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
④方程f(x)=
| 1 |
| 2 |
其中正确命题的序号是 ①④.
故答案为:①④.
点评:本题以三角函数和新定义的函数为例,考查了函数的周期性、单调性、对称性、函数零点与方程根的个数的讨论等知识点,属于中档题.采用数形结合法,是解决本题的关键.

练习册系列答案
相关题目
 ,则称m为x的“亲密整数”,记作{x},即{x}=m,已知函数f(x)=x-{x}.给出以下四个命题:
,则称m为x的“亲密整数”,记作{x},即{x}=m,已知函数f(x)=x-{x}.给出以下四个命题: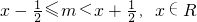 ,则称m为x的“亲密整数”,记作{x},即{x}=m,已知函数f(x)x-{x}.给出以下四个命题:
,则称m为x的“亲密整数”,记作{x},即{x}=m,已知函数f(x)x-{x}.给出以下四个命题: 上单调递增;
上单调递增;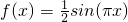 在[-2,2]上共有7个不相等的实数根.
在[-2,2]上共有7个不相等的实数根. ,则称m为x的“亲密整数”,记作{x},即{x}=m,已知函数f(x)x-{x}.给出以下四个命题:
,则称m为x的“亲密整数”,记作{x},即{x}=m,已知函数f(x)x-{x}.给出以下四个命题: 上单调递增;
上单调递增; 在[-2,2]上共有7个不相等的实数根.
在[-2,2]上共有7个不相等的实数根. ,则称m为x的“亲密整数”,记作{x},即{x}=m,已知函数f(x)x﹣{x}.给出以下四个命题:
,则称m为x的“亲密整数”,记作{x},即{x}=m,已知函数f(x)x﹣{x}.给出以下四个命题: 上单调递增;
上单调递增; 在[﹣2,2]上共有7个不相等的实数根.
在[﹣2,2]上共有7个不相等的实数根.