题目内容
已知函数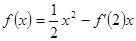 ,
,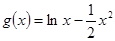 。
。
(1)求函数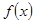 的解析式;
的解析式;
(2)若对于任意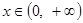 ,都有
,都有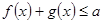 成立,求实数
成立,求实数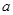 的取值范围;
的取值范围;
(3)设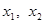 ,
,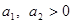 ,且
,且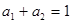 ,求证:
,求证: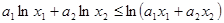 。
。
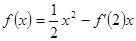 ,
,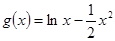 。
。(1)求函数
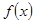 的解析式;
的解析式;(2)若对于任意
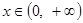 ,都有
,都有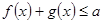 成立,求实数
成立,求实数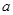 的取值范围;
的取值范围;(3)设
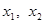 ,
,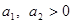 ,且
,且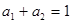 ,求证:
,求证: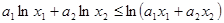 。
。(1)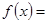
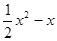 ,(2)
,(2)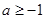 ,(3)详见解析
,(3)详见解析
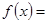
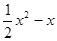 ,(2)
,(2)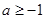 ,(3)详见解析
,(3)详见解析试题分析:(1)本题中的参数为
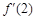 ,利用导函数构造关于
,利用导函数构造关于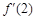 的方程. 因为
的方程. 因为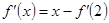 ,所以
,所以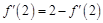 ,
,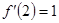 ,故
,故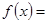
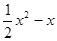 ,(2)不等式恒成立问题,往往转化为最值问题,即
,(2)不等式恒成立问题,往往转化为最值问题,即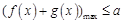 ,本题实质求函数
,本题实质求函数 在
在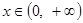 上最大值. 因为
上最大值. 因为 ,所以
,所以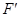
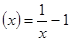 ,因此当时
,因此当时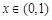 单调增,当
单调增,当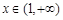 时单调减,所以当
时单调减,所以当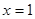 时,
时,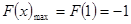 ,从而
,从而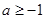 .(3)证明不等式先要观察其结构特点,原不等式结构虽对称,但不可分离,需要适当变形.利用
.(3)证明不等式先要观察其结构特点,原不等式结构虽对称,但不可分离,需要适当变形.利用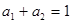 ,将原不等式等价变形为
,将原不等式等价变形为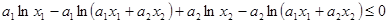 ,即
,即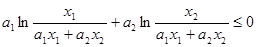
利用(II)结论
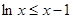 ,
,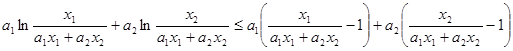 =0
=0试题解析:(1)解:因为
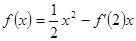 ,所以
,所以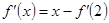 。
。令
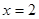 ,得
,得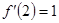 ,所以
,所以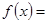
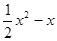 。 3分
。 3分(2)解:设
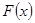
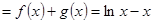 ,
,则
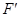
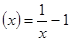 ,令
,令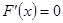 ,解得
,解得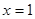 。
。当
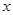 变化时,
变化时,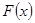 与
与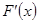 的变化情况如下表:
的变化情况如下表: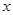 | (0,1) | 1 | 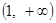 |
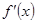 | + | 0 | - |
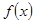 | 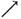 | 极大值 | 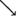 |
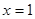 时,
时,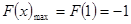 。
。因为对于任意
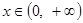 ,都有
,都有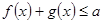 成立,
成立,所以
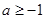 。 7分
。 7分(3)证明:由(II),得
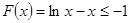 ,即
,即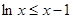 ,
,令
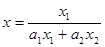 ,得
,得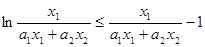 ,
,令
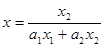 ,得
,得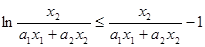 ,
,所以
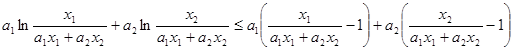
因为
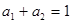 ,
,所以
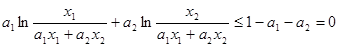 ,
,即
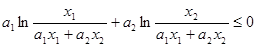 ,
,所以
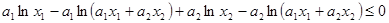 ,
,即
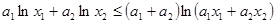 ,
,所以
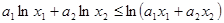 。 12分
。 12分
练习册系列答案
相关题目

 ,求函数
,求函数 在
在 上的最小值;
上的最小值; 存在单调递增区间,试求实数
存在单调递增区间,试求实数 的取值范围;
的取值范围;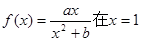 处取得极值2
处取得极值2 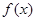 的表达式;
的表达式;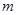 满足什么条件时,函数
满足什么条件时,函数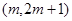 上单调递增?
上单调递增?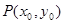 为
为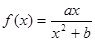 图象上任意一点,直线与
图象上任意一点,直线与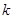 的取值范围
的取值范围  ,
, ,
,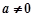 .
. 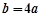 ,求
,求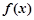 的单调递增区间;
的单调递增区间; 与
与 轴相切于异于原点的一点,且
轴相切于异于原点的一点,且 ,求
,求 的值.
的值.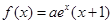 (其中
(其中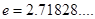 ),
),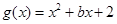 ,已知它们在
,已知它们在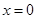 处有相同的切线.
处有相同的切线.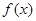 ,
,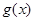 的解析式;
的解析式; 上的最小值;
上的最小值;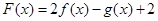 零点个数.
零点个数.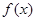 与
与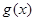 是定义在
是定义在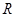 上的两个可导函数,若
上的两个可导函数,若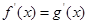 ,则
,则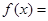
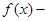
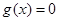
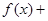
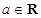 ,函数
,函数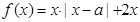 .
.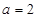 ,求函数
,求函数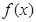 在区间
在区间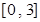 上的最大值;
上的最大值;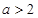 ,写出函数
,写出函数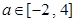 ,使得关于
,使得关于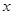 的方程
的方程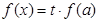 有三个不相等的实数解,求实数
有三个不相等的实数解,求实数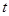 的取值范围.
的取值范围.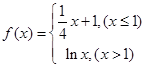 则方程
则方程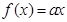 恰有两个不同的实根时,实数a的取值范围是(注:e为自然对数的底数)( )
恰有两个不同的实根时,实数a的取值范围是(注:e为自然对数的底数)( )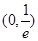
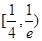
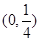
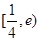
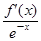 -a-2,h(x)=
-a-2,h(x)=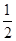 x2-2x-ln x,若x>1时总有g(x)<h(x),求实数a的取值范围.
x2-2x-ln x,若x>1时总有g(x)<h(x),求实数a的取值范围.