题目内容
设函数
(1)若 ,求函数
,求函数 在
在 上的最小值;
上的最小值;
(2)若函数 在
在 存在单调递增区间,试求实数
存在单调递增区间,试求实数 的取值范围;
的取值范围;
(3)求函数 的极值点.
的极值点.

(1)若
 ,求函数
,求函数 在
在 上的最小值;
上的最小值;(2)若函数
 在
在 存在单调递增区间,试求实数
存在单调递增区间,试求实数 的取值范围;
的取值范围;(3)求函数
 的极值点.
的极值点.(1)最小值为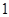 .(2)
.(2)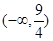 .
.
(3)当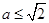 时,函数
时,函数 没有极值点;
没有极值点;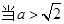 时,
时,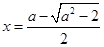 是函数
是函数 的极大值点;
的极大值点;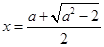 是函数
是函数 的极小值点.
的极小值点.
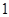 .(2)
.(2)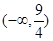 .
.(3)当
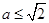 时,函数
时,函数 没有极值点;
没有极值点;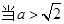 时,
时,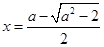 是函数
是函数 的极大值点;
的极大值点;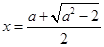 是函数
是函数 的极小值点.
的极小值点.试题分析:(1)
 的定义域为
的定义域为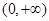 ,根据
,根据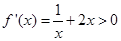 ,得
,得 在
在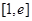 上增函数,当
上增函数,当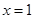 时,
时, 取得最小值
取得最小值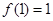 .
.(2)由于
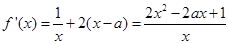 ,设
,设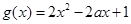 .
.依题意,在区间
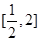 上存在子区间使得不等式
上存在子区间使得不等式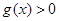 成立.
成立.根据
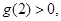 或
或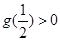 ,解得实数
,解得实数 取值范围是
取值范围是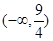 .
.(3)由
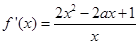 ,令
,令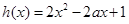 .分
.分 ,
,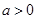 讨论
讨论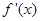 的符号及驻点情况.
的符号及驻点情况.1)当
 时,在
时,在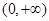 上
上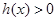 恒成立,
恒成立,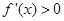 ,此时,函数
,此时,函数 没有极值点.
没有极值点.2)当
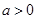 时,
时,①当
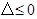 即
即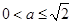 时,在
时,在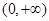 上
上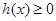 恒成立,这时
恒成立,这时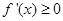 ,此时,函数
,此时,函数 没有极值点.
没有极值点.②当
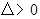 即
即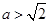 时,
时,当
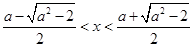 时,易知
时,易知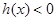 ,这时
,这时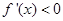 ;
;当
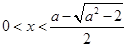 或
或 时,易知
时,易知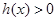 ,这时
,这时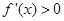 .
.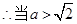 时,
时,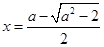 是函数
是函数 的极大值点;
的极大值点;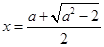 是函数
是函数 的极小值点.
的极小值点.解答本题的主要难度在于转化思想与分类讨论思想的利用.
试题解析:(1)
 的定义域为
的定义域为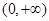 ,
,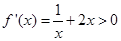 ,
,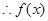 在
在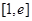 上增函数,当
上增函数,当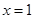 时,
时, 取得最小值
取得最小值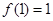 ,
,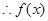 在
在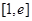 上的最小值为
上的最小值为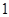 . 4分
. 4分(2)
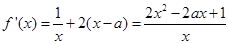 ,设
,设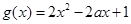 .
.依题意,在区间
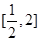 上存在子区间使得不等式
上存在子区间使得不等式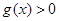 成立.
成立.注意到抛物线
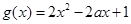 开口向上,所以只要
开口向上,所以只要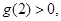 或
或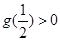 即可.
即可.由
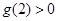 得
得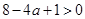 ,解得
,解得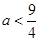 ,
,由
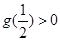 得
得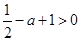 ,得
,得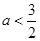 ,
,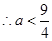 ,即实数
,即实数 取值范围是
取值范围是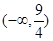 . 8分
. 8分(3)
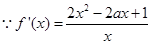 ,令
,令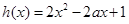 。
。1)显然,当
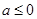 时,在
时,在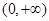 上
上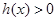 恒成立,这时
恒成立,这时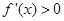 ,此时,函数
,此时,函数 没有极值点.
没有极值点.2)当
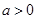 时,
时,①当
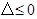 即
即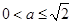 时,在
时,在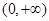 上
上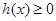 恒成立,这时
恒成立,这时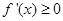 ,此时,函数
,此时,函数 没有极值点.
没有极值点.②当
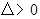 即
即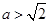 时,
时,当
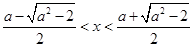 时,易知
时,易知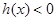 ,这时
,这时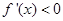 ;
;当
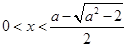 或
或 时,易知
时,易知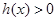 ,这时
,这时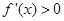 .
.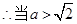 时,
时,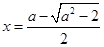 是函数
是函数 的极大值点;
的极大值点;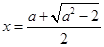 是函数
是函数 的极小值点.
的极小值点.综上,当
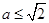 时,函数
时,函数 没有极值点;
没有极值点;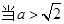 时,
时,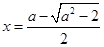 是函数
是函数 的极大值点;
的极大值点;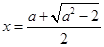 是函数
是函数 的极小值点. 13分
的极小值点. 13分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
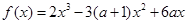
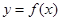 在点(2,f (2))处的切线方程;
在点(2,f (2))处的切线方程;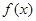 在闭区间[0,|2a|]上的最小值.
在闭区间[0,|2a|]上的最小值.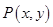 为函数
为函数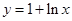 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线 的斜率
的斜率 .
.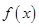 在区间
在区间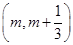
 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围;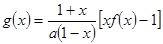 ,若对任意
,若对任意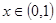 恒有
恒有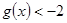 ,求实数
,求实数 的取值范围.
的取值范围. 是自然对数的底数,函数
是自然对数的底数,函数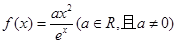 .
. 的单调递增区间;
的单调递增区间;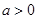 时,函数
时,函数 ,求
,求 的值.
的值.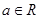 ),
),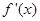 是f(x)的导函数.
是f(x)的导函数.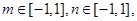 求
求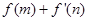 的最小值;
的最小值;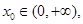 使f(x0)>0,求a的取值范围.
使f(x0)>0,求a的取值范围.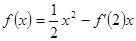 ,
,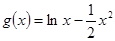 。
。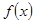 的解析式;
的解析式;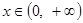 ,都有
,都有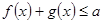 成立,求实数
成立,求实数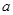 的取值范围;
的取值范围;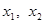 ,
,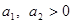 ,且
,且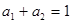 ,求证:
,求证: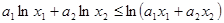 。
。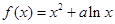 图象与直线
图象与直线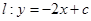 相切,切点横坐标为
相切,切点横坐标为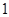 .
.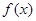 的表达式和直线
的表达式和直线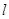 的方程;(2)求函数
的方程;(2)求函数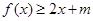 对
对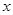 恒成立,求实数
恒成立,求实数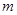 的取值范围.
的取值范围.