题目内容
2.已知函数f(x)=ax2+bx+ln(x+1)(a,b∈R)的图象在点(1,f(1))处的切线方程为5x+2y-2ln2-1=0.(1)求实数a的值以及函数y=f(x)的极值;
(2)若函数y=f(x)(x∈[0,2])的图象与直线y=-$\frac{5}{2}$x+m恰有两个公共点,求实数m的取值范围;
(3)证明:ln(n+1)<$\frac{2}{{1}^{2}}$+$\frac{3}{{2}^{2}}$+…+$\frac{n+1}{{n}^{2}}$(n∈N*)
分析 (1)求出导数,求得切线的斜率和切点,由切线方程可得a,b的方程,解得a,b,再由导数大于0,可得增区间,导数小于0,可得减区间,进而得到极值;
(2)由题意可得m-$\frac{5}{2}$x=-x2-x+ln(x+1)在[0,2]上有两解,则m=ln(x+1)-x2+$\frac{3}{2}$x,令g(x)=ln(x+1)-x2+$\frac{3}{2}$x,求得g(x)在[0,2]的值域,即可得到所求m的范围;
(3)求得f(x)的导数,求得x>0的单调性,再令x=$\frac{1}{n}$,由对数的运算性质,即可得证.
解答 解:(1)函数f(x)=ax2+bx+ln(x+1)的导数为
f′(x)=2ax+b+$\frac{1}{x+1}$,
在点(1,f(1))处的切线斜率为2a+b+$\frac{1}{2}$=-$\frac{5}{2}$,
即为2a+b=-3,
又f(1)=a+b+ln2=ln2-2.即为a+b=-2.
解得a=b=-1,
则f(x)=-x2-x+ln(x+1),x>-1.
f′(x)=-2x-1+$\frac{1}{x+1}$=$\frac{-x(2x+3)}{x+1}$,
当-1<x<0时,f′(x)>0,f(x)递增;
当x>0时,f′(x)<0,f(x)递减.
则f(x)在x=0处取得极大值,且为0;
没有极小值;
(2)由题意可得,m-$\frac{5}{2}$x=-x2-x+ln(x+1)在[0,2]上有两解,
则m=ln(x+1)-x2+$\frac{3}{2}$x,
令g(x)=ln(x+1)-x2+$\frac{3}{2}$x,则g′(x)=$\frac{1}{x+1}$-2x+$\frac{3}{2}$=$\frac{-(x-1)(4x+5)}{2(x+1)}$,
当1<x<2时,g′(x)<0,g(x)递减;当0<x<1时,g′(x)>0,g(x)递增.
即有x=1处取得极大值,且为最大值ln2+$\frac{1}{2}$,
由g(0)=0,g(2)=ln3-1,
即有实数m的取值范围为[ln3-1,ln2+$\frac{1}{2}$);
(3)证明:f(x)=-x2-x+ln(x+1),x>-1.
f′(x)=-2x-1+$\frac{1}{x+1}$=$\frac{-x(2x+1)}{x+1}$,
当x>0时,f′(x)<0,即f(x)在(0,+∞)递减,
即有f(x)<f(0)=0,
即为-x2-x+ln(x+1)<0.
则ln(x+1)<x2+x,
令x=$\frac{1}{n}$,则ln(1+$\frac{1}{n}$)<$\frac{1}{{n}^{2}}$+$\frac{1}{n}$=$\frac{n+1}{{n}^{2}}$,
即有ln$\frac{2}{1}$+ln$\frac{3}{2}$+…+ln$\frac{n+1}{n}$<$\frac{2}{{1}^{2}}$+$\frac{3}{{2}^{2}}$+…+$\frac{n+1}{{n}^{2}}$,
即为ln($\frac{2}{1}$•$\frac{3}{2}$…$\frac{n+1}{n}$)<$\frac{2}{{1}^{2}}$+$\frac{3}{{2}^{2}}$+…+$\frac{n+1}{{n}^{2}}$,
即有ln(n+1)<$\frac{2}{{1}^{2}}$+$\frac{3}{{2}^{2}}$+…+$\frac{n+1}{{n}^{2}}$(n∈N*).
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查函数和方程的转化思想和不等式的证明,注意运用函数的单调性和对数的运算性质,属于中档题.

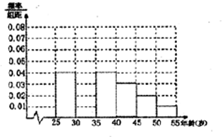 某班同学利用劳动节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
某班同学利用劳动节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55) | 15 | 0.3 |
(2)请根据(1)中补全的频率分布直方图求抽取n的人的年龄的众数和中位数的估计值.