题目内容
已知向量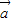 =(cosx,sinx),
=(cosx,sinx),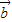 =(-cosx,cosx),
=(-cosx,cosx),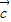 =(-1,0).
=(-1,0).(Ⅰ)若
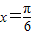 ,求向量
,求向量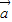 、
、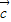 的夹角;
的夹角;(Ⅱ)当
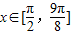 时,求函数
时,求函数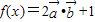 的最大值.
的最大值.
【答案】分析:(Ⅰ)先求出向量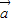 、
、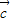 的坐标,及向量的模,代入两个向量的夹角公式进行运算.
的坐标,及向量的模,代入两个向量的夹角公式进行运算.
(Ⅱ)利用两个向量的数量积公式及三角公式,把函数的解析式化为某个角三角函数的形式,根据角的范围,结合
三角函数的单调性求出函数的值域.
解答:解:(Ⅰ)当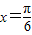 时,
时,
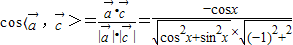 =
=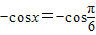
=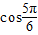 ,∵
,∵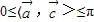 ,∴
,∴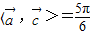 .
.
(Ⅱ)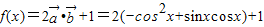 =2sinxcosx-(2cos2x-1)
=2sinxcosx-(2cos2x-1)
=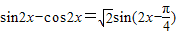 ,
,
∵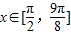 ,∴
,∴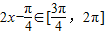 ,故
,故 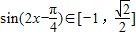 ,
,
∴当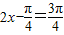 ,
,
即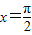 时,f(x)max =1.
时,f(x)max =1.
点评:本意考查两个向量的夹角公式,两个向量的数量积运算以及三角公式的应用,利用三角函数的单调性、有界性求其值域.
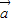 、
、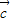 的坐标,及向量的模,代入两个向量的夹角公式进行运算.
的坐标,及向量的模,代入两个向量的夹角公式进行运算.(Ⅱ)利用两个向量的数量积公式及三角公式,把函数的解析式化为某个角三角函数的形式,根据角的范围,结合
三角函数的单调性求出函数的值域.
解答:解:(Ⅰ)当
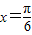 时,
时,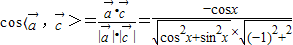 =
=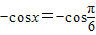
=
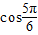 ,∵
,∵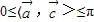 ,∴
,∴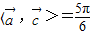 .
.(Ⅱ)
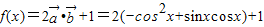 =2sinxcosx-(2cos2x-1)
=2sinxcosx-(2cos2x-1) =
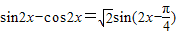 ,
,∵
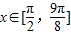 ,∴
,∴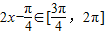 ,故
,故 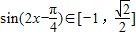 ,
,∴当
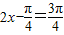 ,
,即
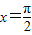 时,f(x)max =1.
时,f(x)max =1.点评:本意考查两个向量的夹角公式,两个向量的数量积运算以及三角公式的应用,利用三角函数的单调性、有界性求其值域.

练习册系列答案
相关题目