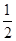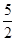题目内容
设函数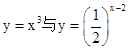 的图像的交点为
的图像的交点为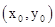 ,则x0所在的区间是
,则x0所在的区间是
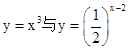 的图像的交点为
的图像的交点为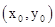 ,则x0所在的区间是
,则x0所在的区间是A.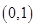 | B.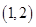 | C.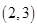 | D.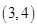 |
B
试题分析:因为根据题意可知,当x=1时,则
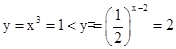 ,而当x=2时,则
,而当x=2时,则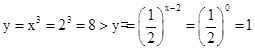 ,并且前者是递增函数,后者是递减函数那么可知必然交点在该区间取得,故选B.
,并且前者是递增函数,后者是递减函数那么可知必然交点在该区间取得,故选B.点评:解决该试题的关键是根据函数的图像与图像的位置关系来判定交点的位置,也可以通过求解各个区间的左右端点值,是否是满足图像出现交的情况即可。

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
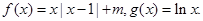 .
.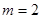 时,求函数
时,求函数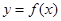 在
在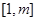 上的最大值;
上的最大值; ,若函数
,若函数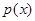 有零点,求
有零点,求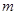 的取值范围.
的取值范围. 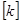 ,即
,即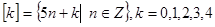 给出四个结论:
给出四个结论: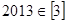 ,②
,②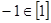 ,③
,③ ,④整数
,④整数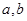 属于同一“类”,当且仅当是
属于同一“类”,当且仅当是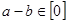 ,其中正确结论的个数是( )
,其中正确结论的个数是( )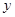 轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里
轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里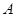 处,如图,现假设:①失事船的移动路径可视为抛物线
处,如图,现假设:①失事船的移动路径可视为抛物线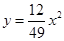 ;②定位后救援船即刻沿直线匀速前往救援;③救援船出发
;②定位后救援船即刻沿直线匀速前往救援;③救援船出发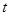 小时后,失事船所在位置的横坐标为
小时后,失事船所在位置的横坐标为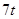

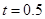 时,写出失事船所在位置
时,写出失事船所在位置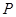 的纵坐标,若此时两船恰好会合,求救援船速度的大小和方向 (若确定方向时涉及到的角为非特殊角,用符号及其满足的条件表示即可)
的纵坐标,若此时两船恰好会合,求救援船速度的大小和方向 (若确定方向时涉及到的角为非特殊角,用符号及其满足的条件表示即可)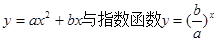 的图象只可能是 ( )
的图象只可能是 ( )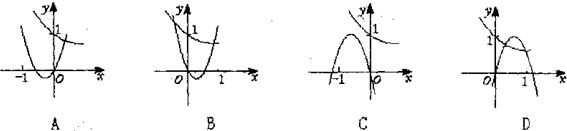
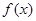 对任意的
对任意的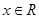 恒有
恒有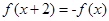 且
且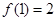 ,则
,则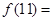 ( )
( )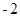

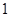
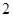
 是偶函数,
是偶函数,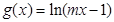 在
在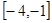 内单调递减,则实数
内单调递减,则实数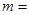 。
。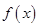 是定义在R上不恒为零的偶函数,且对任意
是定义在R上不恒为零的偶函数,且对任意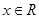 ,都有
,都有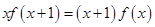 ,则
,则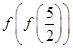 的值是( )
的值是( )