题目内容
(本题满分12分)
已知 是一个公差大于
是一个公差大于 的等差数列,且满足
的等差数列,且满足 .数列
.数列 ,
, ,
, ,…,
,…, 是首项为
是首项为 ,公比为
,公比为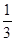 的等比数列.
的等比数列.
(1) 求数列 的通项公式;
的通项公式;
(2) 若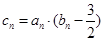 ,求数列
,求数列 的前
的前 项和
项和 .
.
(1) 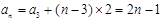 ;(2)
;(2)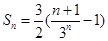 .
.
解析(Ⅰ)设等差数列{an}的公差为d,d>0,利用等差数列的通项表示已知,求解出d,a1,结合等差数列的通项即可求解
(Ⅱ)数列 ,
, ,
, ,…,
,…, 是首项为
是首项为 ,公比为
,公比为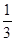 的等比数列.得到
的等比数列.得到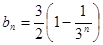 ,
,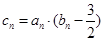
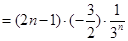 ,,结合数列的特点,考虑利用错位相减求解数列的和。
,,结合数列的特点,考虑利用错位相减求解数列的和。
解: (1) 解: 设等差数列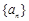 的公差为
的公差为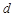 , 则依题知
, 则依题知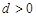 ,
,
由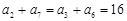 且
且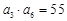 得
得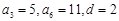
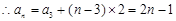 ; ……………………………………………………………………4分
; ……………………………………………………………………4分
(2) 由(1)得: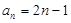 (
(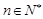 ).
).
b1=1,当n≥2时,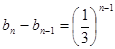 ,
,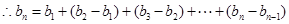
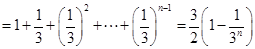
因而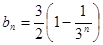 ,
,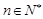 .
. 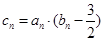
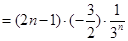 ,…………………………7分
,…………………………7分
∴
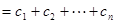
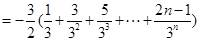
令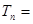
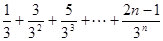 ①
①
则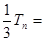
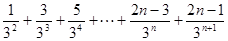 ②
②
①-②得: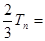
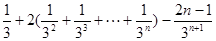
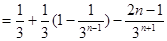 ……………………………10分
……………………………10分
∴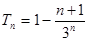 .∴
.∴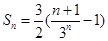 . …………………………………………………………12分
. …………………………………………………………12分

练习册系列答案
相关题目
 }的前n项和为
}的前n项和为 ,已知
,已知 ,
, .
.
 ,求数列{
,求数列{ }的前项和
}的前项和 .
. 中的数按上小下大、左小右大的原则排成如下三角形数表:
中的数按上小下大、左小右大的原则排成如下三角形数表:
 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行、从左往右数第
行、从左往右数第 个数.
个数. ,求
,求 的值;
的值; ,求证
,求证 .(本题满分14分)
.(本题满分14分) 的公差大于0,且
的公差大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前
的前 项的和为
项的和为 ,且
,且 .
. ,求证:
,求证: ;
; 的前
的前 .
. 是等差数列,
是等差数列,
 ,求数列
,求数列 的前n项和Sn.
的前n项和Sn. 的前n项和为
的前n项和为 ,点
,点 均在函数y=-x+12的图像上.
均在函数y=-x+12的图像上. 是公差不为零的等差数列,
是公差不为零的等差数列,  成等比数列.
成等比数列. 的前n项和
的前n项和
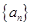 满足:
满足: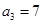 ,
,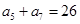 ,
, .
.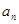 及
及 (
(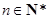 ),求数列
),求数列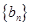 的前n项和
的前n项和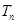 .
. 的前n项和为
的前n项和为 ,且
,且
 ,试求数列
,试求数列 的前
的前 项和.
项和.