题目内容
【题目】在平面直角坐标系xoy中,动点M到点F(1,0)的距离与它到直线x=2的距离之比为 ![]() . (Ⅰ)求动点M的轨迹E的方程;
. (Ⅰ)求动点M的轨迹E的方程;
(Ⅱ)设直线y=kx+m(m≠0)与曲线E交于A,B两点,与x轴、y轴分别交于C,D两点(且C,D在A,B之间或同时在A,B之外).问:是否存在定值k,对于满足条件的任意实数m,都有△OAC的面积与△OBD的面积相等,若存在,求k的值;若不存在,说明理由.
【答案】解:(Ⅰ)设M(x,y),由题意可得 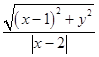 =
= ![]() , 两边平方可得x2+y2﹣2x+1=
, 两边平方可得x2+y2﹣2x+1= ![]() (x2﹣4x+4),
(x2﹣4x+4),
即有 ![]() +y2=1,
+y2=1,
可得轨迹E的方程为 ![]() +y2=1;
+y2=1;
(Ⅱ)联立 ![]() ,消去y,可得(1+2k2)x2+4kmx+2m2﹣2=0,
,消去y,可得(1+2k2)x2+4kmx+2m2﹣2=0,
△=16k2m2﹣4(1+2k2)(2m2﹣2)=8(2k2﹣m2+1),
由△>0,可得m2<1+2k2(*),
设A(x1 , y1),B(x2 , y2),则x1+x2=﹣ ![]() ,
,
由题意可设C(﹣ ![]() ,0),D(0,m),
,0),D(0,m),
△OAC的面积与△OBD的面积相等|AC|=|BD|恒成立
线段AB的中点和线段CD中点重合.
即有﹣ ![]() =﹣
=﹣ ![]() ,解得k=±
,解得k=± ![]() ,
,
即存在定值k=± ![]() ,对于满足条件的m≠0,且|m|<
,对于满足条件的m≠0,且|m|< ![]()
的任意实数m,都有△OAC的面积与△OBD的面积相等
【解析】(Ⅰ)设M(x,y),运用两点的距离公式和点到直线的距离公式,两边平方整理即可得到所求轨迹E的方程;(Ⅱ)联立直线方程和椭圆方程,消去y,可得x的方程,运用判别式大于0,以及韦达定理,求得C,D的坐标,由△OAC的面积与△OBD的面积相等|AC|=|BD|恒成立线段AB的中点和线段CD中点重合.运用中点坐标公式,解方程可得k的值,即可判断存在.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目