题目内容
17.数列{an}中,an>0,若S12,S22,…,Sn2,…是一个以1为首项,2为公差的等差数列,求an.分析 由已知求出${S}_{n}=\sqrt{2n-1}$.求出a1,再利用an=Sn-Sn-1(n≥2)求得答案.
解答 解:∵S12,S22,…,Sn2,…是一个以1为首项,2为公差的等差数列,
∴${{S}_{n}}^{2}=1+2(n-1)=2n-1$,
∵an>0,
∴${S}_{n}=\sqrt{2n-1}$.
当n=1时,a1=S1=1;
当n≥2时,an=Sn-Sn-1=$\sqrt{2n-1}-\sqrt{2(n-1)-1}$=$\sqrt{2n-1}-\sqrt{2n-3}$.
a1=1不适合上式.
∴${a}_{n}=\left\{\begin{array}{l}{1,n=1}\\{\sqrt{2n-1}-\sqrt{2n-3},n≥2}\end{array}\right.$.
点评 本题考查等差数列的通项公式,训练了利用数列的前n项和求数列的通项公式,是基础题.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
12.若f(x)=5-3x(2<x≤4),则f(x)的值域为( )
| A. | R | B. | [-7,-1) | C. | (-7,-1] | D. | {-7,-1} |
9.数列{1+2n-1}的前n项的和为( )
| A. | 1+2n | B. | 2+2n | C. | n+2n-1 | D. | n+2+2n |
6.利用计算机在区间(0,1)上产生两个随机数a和b,则关于x的方程x2+2ax+b=0有实根的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
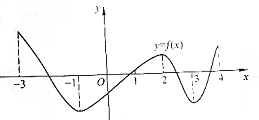 已知函数y=f(x)在区间[-3,4]上的图象如图所示,根据图象说出函数的单调区间,以及在每一个区间上函数的单调性.
已知函数y=f(x)在区间[-3,4]上的图象如图所示,根据图象说出函数的单调区间,以及在每一个区间上函数的单调性.