题目内容
为预防H7N9病毒爆发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
| 分组 | A组 | B组 | C组 |
| 疫苗有效 | 673 | a | b |
| 疫苗无效 | 77 | 90 | c |
(I)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取样本多少个?
(II)已知b≥465,c ≥30,求通过测试的概率
(I)90;(II)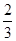 .
.
解析试题分析:(I)由古典概型的概率公式,可得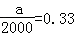 ,求
,求 ,从而可求C组样本个数
,从而可求C组样本个数 ,然后根据分层抽样抽样比为
,然后根据分层抽样抽样比为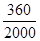 ,故可确定在C组抽取样本个数为
,故可确定在C组抽取样本个数为 ;(II)由(I)知
;(II)由(I)知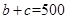 ,结合已知条件,可确定满足条件的
,结合已知条件,可确定满足条件的 的取值有6种,测试没有通过相当于疫苗无效的概率大于
的取值有6种,测试没有通过相当于疫苗无效的概率大于 ,从而求出
,从而求出 的范围,进而可求出没有通过测试的基本事件数,利用对立事件的概率公式求解.
的范围,进而可求出没有通过测试的基本事件数,利用对立事件的概率公式求解.
试题解析:(I)∵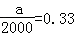 ,∴a=660,∵b+c=2000﹣673﹣77﹣660﹣90=500,∴应在C组抽取样个数是
,∴a=660,∵b+c=2000﹣673﹣77﹣660﹣90=500,∴应在C组抽取样个数是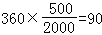 (个);
(个);
(II)∵b+c=500,b≥465,c≥30,∴(b,c)的可能是:(465,35),(466,34),(467,33),(468,32),(469,31),(470,30),若测试没有通过,则77+90+c>2000×(1﹣90%)=200,c>33,
(b,c)的可能性是(465,35),(466,34),通过测试的概率是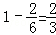 .
.
考点:1、分层抽样;2、古典概型求概率.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
某学校100名学生期中考试语文成绩的频率分布直方图如下右图所示,其中成绩分组区间是: ,
, ,
, ,
, ,
, 。
。
求图中a的值;
根据频率分布直方图,估计这100名学生语文成绩的平均分;
若这100名学生语文成绩某些分数段的人数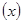 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数
之比如下表所示,求数学成绩在 之外的人数。
之外的人数。
| 分数段 |  | 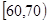 |  | 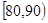 |
x :y :y | 1:1 | 2:1 | 3:4 | 4:5 |
为了调查某大学学生在周日上网的时间,随机对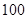 名男生和
名男生和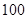 名女生进行了不记名的问卷调查,得到了如下的统计结果:
名女生进行了不记名的问卷调查,得到了如下的统计结果:
表1:男生上网时间与频数分布表
| 上网时间(分钟) | 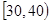 | 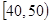 | 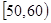 |  | 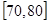 |
| 人数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间(分钟) | 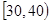 | 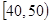 | 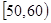 |  | 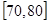 |
| 人数 | 10 | 20 | 40 | 20 | 10 |
(Ⅱ)完成表3的
 列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?
列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?(Ⅲ)从表3的男生中“上网时间少于60分钟”和“上网时间不少于60分钟”的人数中用分层抽样的方法抽取一个容量为5的样本,再从中任取两人,求至少有一人上网时间超过60分钟的概率.
表3 :
| | 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 |
| 男生 | | | |
| 女生 | | | |
| 合计 | | | |
 ,其中
,其中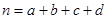
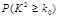 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
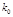 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
 ,
, ,
, ,
, ,
,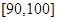 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在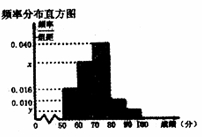

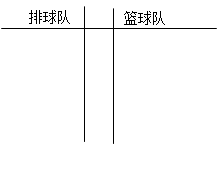
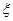 表示所抽取的3名同学中得分在
表示所抽取的3名同学中得分在 名同学,现测得排球队
名同学,现测得排球队 )分别是:
)分别是: 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、


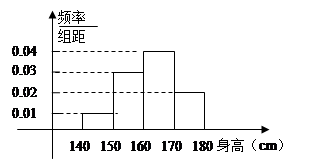
 (简称血酒含量,单位是毫克/
(简称血酒含量,单位是毫克/ 毫升),当
毫升),当 时,为“酒后驾车”;当
时,为“酒后驾车”;当 时,为“醉酒驾车”.某市公安局交通管理部门于
时,为“醉酒驾车”.某市公安局交通管理部门于 年
年 月的某天晚上
月的某天晚上 点至
点至 名饮酒后违法驾驶机动车者,如图为这
名饮酒后违法驾驶机动车者,如图为这 的人数计入
的人数计入 人数之内).
人数之内).
 人,求
人,求 人为“酒后驾车”另
人为“酒后驾车”另