题目内容
已知函数f(x)＝ln x－ax＋1在x＝2处的切线斜率为－
.
(1)求实数a的值及函数f(x)的单调区间；
(2)设g(x)＝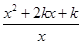
，对?x1∈(0，＋∞)，?x2∈(－∞，0)使得f(x1)≤g(x2)成立，求正实数k的取值范围；
(3)证明：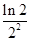
＋
＋…＋
<
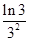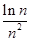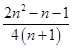(n∈N*，n≥2)．
（1）即f(x)的单调递增区间为(0,1)，单调递减区间为(1，＋∞)．
（2）k≥1
（3）见解析
解析
练习册系列答案
相关题目
题目内容
已知函数f(x)＝ln x－ax＋1在x＝2处的切线斜率为－.
(1)求实数a的值及函数f(x)的单调区间；
(2)设g(x)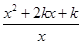＝，对?x1∈(0，＋∞)，?x2∈(－∞，0)使得f(x1)≤g(x2)成立，求正实数k的取值范围；
(3)证明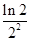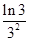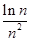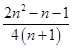： ＋＋…＋<(n∈N*，n≥2)．
（1）即f(x)的单调递增区间为(0,1)，单调递减区间为(1，＋∞)．
（2）k≥1
（3）见解析
解析
的最大值；
，求
的取值范围.
+
（n
）
在x=1处有极小值－1，
的值; (2)求出
的单调区间.
．若曲线
在点
处的切线与直线
垂直，
的值；
的单调区间；
.
时，设
.讨论函数
的单调性；
.
在点(1,0)处的切线．
(单位：千克)与销售价格
(单位：元/千克)满足关系式
，其中
，
为常数.已知销售价格为5元/千克时，每日可售出该商品11千克．