题目内容
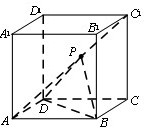 如图,P是正方体ABCD-A1B1C1D1对角线AC1上一动点,设AP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( )
如图,P是正方体ABCD-A1B1C1D1对角线AC1上一动点,设AP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( )分析:先设正方体的棱长为1,连接AC交BD于O,连PO,则PO是等腰△PBD的高,从而△PBD的面积为f(x)=
BD×PO,再在在三角形PAO中,利用余弦定理得出PO,最后得出f(x)的解析式,画出其图象,对照选项即可解决问题.
| 1 |
| 2 |
解答: 解:设正方体的棱长为1,连接AC交BD于O,连PO,则PO是等腰△PBD的高,
解:设正方体的棱长为1,连接AC交BD于O,连PO,则PO是等腰△PBD的高,
故△PBD的面积为f(x)=
BD×PO,
在三角形PAO中,PO=
=
,
∴f(x)=
×
×
=
,
画出其图象,如图所示,
对照选项,A正确.
故选A.
 解:设正方体的棱长为1,连接AC交BD于O,连PO,则PO是等腰△PBD的高,
解:设正方体的棱长为1,连接AC交BD于O,连PO,则PO是等腰△PBD的高,故△PBD的面积为f(x)=
| 1 |
| 2 |
在三角形PAO中,PO=
| PA2+AO2-2PA×AOcos∠PAO |
x2+
|
∴f(x)=
| 1 |
| 2 |
| 2 |
x2+
|
| ||
| 2 |
x2-
|
画出其图象,如图所示,
对照选项,A正确.
故选A.
点评:本小题主要考查棱柱的结构特征、函数的图象等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
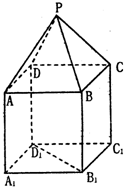 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=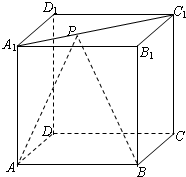 如图,P是正方体ABCD-A1B1C1D1表面对角线A1C1上的一个动点,正方体的棱长为1.
如图,P是正方体ABCD-A1B1C1D1表面对角线A1C1上的一个动点,正方体的棱长为1.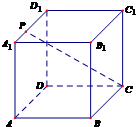 如图所示,已知点P是正方体ABCD-A1B1C1D1的棱A1D1上的一个动点,设异面直线AB与CP所成的角为α,则cosα的最小值是
如图所示,已知点P是正方体ABCD-A1B1C1D1的棱A1D1上的一个动点,设异面直线AB与CP所成的角为α,则cosα的最小值是 如图,P是正方体ABCD-A1B1C1D1表面对角线A1C1上的一个动点,正方体的棱长为1.
如图,P是正方体ABCD-A1B1C1D1表面对角线A1C1上的一个动点,正方体的棱长为1.