题目内容
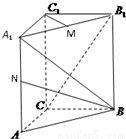
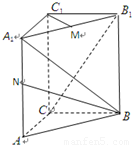
如图,直三棱柱ABCA1B1C1的底面ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.(1)求
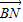 的模;
的模;(2)求异面直线BA1与CB1所成角的余弦值;
(3)求证:A1B⊥C1M.
【答案】分析:(1)建立空间直角坐标系,求出B,N两点的坐标,代入空间两点间的距离公式,即可求出BN的长;
(2)求出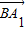 =(1,-1,2),
=(1,-1,2),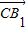 =(0,1,2),利用向量的夹角公式,即可求异面直线BA1与CB1所成角的余弦值;
=(0,1,2),利用向量的夹角公式,即可求异面直线BA1与CB1所成角的余弦值;
(3)证明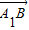 •
•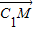 =0,即可证明A1B⊥C1M.
=0,即可证明A1B⊥C1M.
解答: (1)解:以C为坐标原点,以
(1)解:以C为坐标原点,以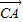 、
、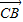 、
、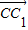 的方向为x轴、y轴、z轴的正方向,建立空间直角坐标系C-xyz,如图
的方向为x轴、y轴、z轴的正方向,建立空间直角坐标系C-xyz,如图
由题意得N(1,0,1),B(0,1,0),
∴|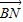 |=
|=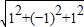 =
=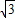 .
.
(2)解:依题意得A1(1,0,2),B(0,1,0),C(0,0,0),B1(0,1,2),C1(0,0,2).
∴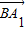 =(1,-1,2),
=(1,-1,2),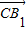 =(0,1,2),
=(0,1,2),
∴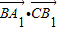 =3.
=3.
∴|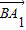 |=
|=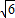 ,|
,|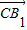 |=
|=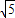 ,
,
∴cos<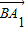 ,
,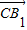 >=
>=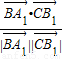 =
=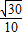 ,
,
∴异面直线BA1与CB1所成角的余弦值为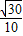 .
.
(3)证明:∵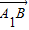 =(-1,1,-2),
=(-1,1,-2),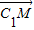 =(
=( ,
, ,0),
,0),
∴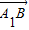 •
•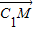 =-1×
=-1× +1×
+1× +(-2)×0=0,
+(-2)×0=0,
∴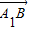 ⊥
⊥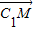 ,即A1B⊥C1M.
,即A1B⊥C1M.
点评:本题考查直线与直线垂直,考查线线角,其中建立空间坐标系,将线线垂直,线线角问题转化为向量夹角问题是解答本题的关键.
(2)求出
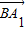 =(1,-1,2),
=(1,-1,2),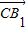 =(0,1,2),利用向量的夹角公式,即可求异面直线BA1与CB1所成角的余弦值;
=(0,1,2),利用向量的夹角公式,即可求异面直线BA1与CB1所成角的余弦值;(3)证明
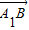 •
•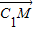 =0,即可证明A1B⊥C1M.
=0,即可证明A1B⊥C1M.解答:
 (1)解:以C为坐标原点,以
(1)解:以C为坐标原点,以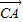 、
、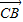 、
、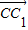 的方向为x轴、y轴、z轴的正方向,建立空间直角坐标系C-xyz,如图
的方向为x轴、y轴、z轴的正方向,建立空间直角坐标系C-xyz,如图由题意得N(1,0,1),B(0,1,0),
∴|
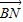 |=
|=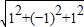 =
=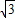 .
.(2)解:依题意得A1(1,0,2),B(0,1,0),C(0,0,0),B1(0,1,2),C1(0,0,2).
∴
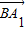 =(1,-1,2),
=(1,-1,2),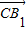 =(0,1,2),
=(0,1,2),∴
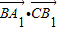 =3.
=3.∴|
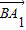 |=
|=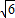 ,|
,|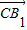 |=
|=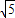 ,
,∴cos<
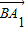 ,
,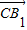 >=
>=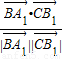 =
=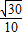 ,
,
∴异面直线BA1与CB1所成角的余弦值为
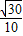 .
.(3)证明:∵
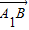 =(-1,1,-2),
=(-1,1,-2),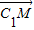 =(
=( ,
, ,0),
,0),∴
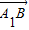 •
•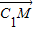 =-1×
=-1× +1×
+1× +(-2)×0=0,
+(-2)×0=0,∴
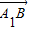 ⊥
⊥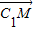 ,即A1B⊥C1M.
,即A1B⊥C1M.点评:本题考查直线与直线垂直,考查线线角,其中建立空间坐标系,将线线垂直,线线角问题转化为向量夹角问题是解答本题的关键.

练习册系列答案
相关题目
 如图,直三棱柱ABC-A1B1C1中,
如图,直三棱柱ABC-A1B1C1中, 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是
如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点. 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.