题目内容
设函数f(x)=![]()
![]() x3-ax2-ax,g(x)=2x2+4x+c.
x3-ax2-ax,g(x)=2x2+4x+c.
(1)试问函数f(x)能否在x=-1时取得极值?说明理由;
(2)若a=-1,当x∈[-3,4]时,函数f(x)与g(x)的图象有两个公共点,求c的取值范围.
(1)不能.由题意f′(x)=x2-2ax-a,
假设在x=-1时f(x)取得极值,则有f′(-1)=1+2a-![]() a=0,∴a=-1,
a=0,∴a=-1,
而此时,f′(x)=x2+2x+1=(x+1)2≥0,函数f(x)在R上为增函数,无极值.
这与f(x)在x=-1有极值矛盾,所以f(x)在x=-1处不能取得极值.
(2)设f(x)=g(x),则有![]() x3-x2-3x-c=0,∴c=
x3-x2-3x-c=0,∴c=![]() x3-x2-3x,
x3-x2-3x,
设F(x)=![]() x3-x2-3x,G(x)=c,令F′(x)=x2-2x-3=0.解得x1=-1或
x3-x2-3x,G(x)=c,令F′(x)=x2-2x-3=0.解得x1=-1或
x=3.
列表如下:
| x | -3 | (-3,-1) | -1 | (-1,3) | 3 | (3,4) | 4 |
| F′(x) | + | 0 | - | 0 | + | ||
| F(x) | -9 |
|
|
| -9 |
| - |
由此可知:F(x)在 (-3,-1)、(3,4)上是增函数,在(-1,3)上是减函数.
当x=-1时,F(x)取得极大值F(-1)=![]() ;当x=3时,F(x)取得极小值F(3)=-9.
;当x=3时,F(x)取得极小值F(3)=-9.
F(-3)=-9,F(4)=-![]() .
.
如果函数f(x)与g(x)的图象有两个公共点,则函数F(x)与G(x)有两个公共点.
所以-![]() <c<
<c<![]() 或c=-
或c=-![]() 9.
9.

练习册系列答案
相关题目
 x3-
x3- x2+a x.
x2+a x.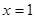 处的切线方程为12x+y-1=0.
处的切线方程为12x+y-1=0. 上的最大值和最小值.
上的最大值和最小值.