题目内容
(12分)设函数f(x)=x3+ax2-9x-1(a<0)若曲线y=f(x)的斜率最小的切线与直线12x+y=6平行。求:
(1)a的值;
(2)函数y=f (x) 的单调区间;
【答案】
(1)f(x)=x3+ax2-9x-1
f '(x)=3x2+2ax-9=3(x+ )2-9-
)2-9-
当x=- 时,f '(x)取得最小值-9-
时,f '(x)取得最小值-9-
∴-9- =-12 即a2=9
=-12 即a2=9
故a=±3 ∵a<0
∴a=-3
(2)由(1)知a=-3,则f(x)=x3-3x2-9x-1
f '(x)=3x2-6x-9=3(x-3)(x + 1)
会f '(x)>0解得x<-1或x>3
会f '(x)<0解得-1<x<3
∴y=f(x)在(-∞,-1)和(3,+∞)上单调递增,在(-1,3)上单调递减。
【解析】略

练习册系列答案
相关题目
 x3-
x3- x2+a x.
x2+a x.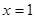 处的切线方程为12x+y-1=0.
处的切线方程为12x+y-1=0. 上的最大值和最小值.
上的最大值和最小值.