题目内容
已知实数a满足1<a≤2,设函数f (x)= x3-
x3- x2+a x.
x2+a x.
(Ⅰ) 当a=2时,求f (x)的极小值;
(Ⅱ) 若函数g(x)=4x3+3bx2-6(b+2)x (b∈R) 的极小值点与f (x)的极小值点相同,
求证:g(x)的极大值小于或等于10.
【答案】
(Ⅰ) 极小值为f (2)=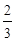 (Ⅱ)证明如下
(Ⅱ)证明如下
【解析】
试题分析:(Ⅰ)解:当a=2时,f ′(x)=x2-3x+2=(x-1)(x-2).
列表如下:
|
x |
(- |
1 |
(1,2) |
2 |
(2,+ |
|
f ′(x) |
+ |
0 |
- |
0 |
+ |
|
f (x) |
单调递增 |
极大值 |
单调递减 |
极小值 |
单调递增 |
所以,f (x)的极小值为f (2)=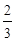 .
.
(Ⅱ) 解:f ′ (x)=x2-(a+1)x+a=(x-1)(x-a).
由于a>1,所以f (x)的极小值点x=a,则g(x)的极小值点也为x=a.
而g′ (x)=12x2+6bx-6(b+2)=6(x-1)(2x+b+2),所以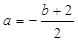 ,
,
即b=-2(a+1).
又因为1<a≤2,所以 g(x)极大值=g(1)=4+3b-6(b+2)=-3b-8=6a-2≤10.
故g(x)的极大值小于或等于10.
考点:导数的应用
点评:导数常应用于求曲线的切线方程、求函数的最值与单调区间、证明不等式和解不等式中参数的取值范围等。

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
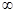 ,1)
,1)