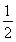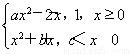题目内容
已知函数f(x)＝ax3－3ax，g(x)＝bx2＋clnx，且g(x)在点(1，g(1))处的切线方程为2y－1＝0.
(1)求g(x)的解析式；
(2)设函数G(x)＝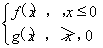
若方程G(x)＝a2有且仅有四个解，求实数a的取值范围．
（1）g(x)＝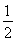
x2－lnx（2）
【解析】(1)g′(x)＝2bx＋
由条件，得
即
∴b＝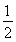
，c＝－1，
∴g(x)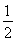＝x2－lnx.
(2)G(x)＝
当x＞0时，G(x)＝g(x)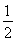＝x2－lnx，g′(x)＝x－
＝
.
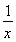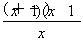令g′(x)＝0，得x＝1，且当x∈(0，1)，g′(x)＜0，x∈(1，＋∞)，g′(x)＞0，
∴g(x)在(0，＋∞)上有极小值，即最小值为g(1)＝.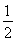
当x≤0时，G(x)＝f(x)＝ax3－3ax，f′(x)＝3ax2－3a＝3a(x＋1)(x－1)．
令f′(x)＝0，得x＝－1.①若a＝0，方程G(x)＝a2不可能有四个解；
②若a＜0时，当x∈(－∞，－1)，f′(x)＜0，当x∈(－1，0)，f′(x)＞0，∴f(x)在(－∞，0]上有极小值，即最小值为f(－1)＝2a.又f(0)＝0，∴G(x)的图象如图①所示，从图象可以看出方程G(x)＝a2不可能有四个解；
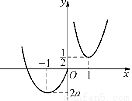,①) 
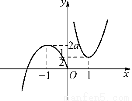,②)
③若a＞0时，当x∈(－∞，－1)，f′(x)＞0，当x∈(－1，0)，f′(x)＜0，∴f(x)在(－∞，0]上有极大值，即最大值为f(－1)＝2a.又f(0)＝0，∴G(x)的图象如图②所示．从图象可以看出方程G(x)＝a2若有四个解，必须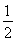＜a2＜2a，∴
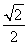＜a＜2.综上所述，满足条件的实数a的取值范围是
练习册系列答案
相关题目
