题目内容
5.若x∈[-2,2],则|x|≤1的概率为$\frac{1}{2}$.分析 本题考查的知识点是几何概型,解题要点是要分别求出满足条件的事件对应的线段长度及总事件对应线段长度.
解答 解:若x∈[-2,2],则|x|≤1,即x∈[-1,1]的概率P=$\frac{1-(-1)}{2-(-2)}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$
点评 几何概型的概率估算公式中的“几何度量”,既可以为本题中的线段长度,也可以包含面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=$\frac{N(A)}{N}$求解.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
15.函数f(x)=$\left\{\begin{array}{l}a{x^2}+x-1(x>2)\\ ax-1(x≤2)\end{array}$是R上的单调递减函数,则实数a的取值范围是( )
| A. | -$\frac{1}{4}$≤a<0 | B. | a≤-$\frac{1}{4}$ | C. | -1≤a≤-$\frac{1}{4}$ | D. | a≤-1 |
17.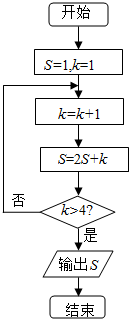 某程序框图如图所示,则输出的结果S等于( )
某程序框图如图所示,则输出的结果S等于( )
 某程序框图如图所示,则输出的结果S等于( )
某程序框图如图所示,则输出的结果S等于( )| A. | 26 | B. | 57 | C. | 60 | D. | 61 |
 已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+2x(x>0)}\\{0(x=0)}\\{{x}^{2}+mx(x<0)}\end{array}\right.$为奇函数.
已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+2x(x>0)}\\{0(x=0)}\\{{x}^{2}+mx(x<0)}\end{array}\right.$为奇函数.