题目内容
3.某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖,若只有1个红球,则获二等奖;若没有红球,则不获奖.(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为X,求X的分布列和数学期望.
分析 (1)记事件A1={从甲箱中摸出一个球是红球},事件A2={从乙箱中摸出一个球是红球},事件B1={顾客抽奖1次获一等奖},事件A2={顾客抽奖1次获二等奖},事件C={顾客抽奖1次能获奖},利用A1,A2相互独立,${A}_{1}\overline{{A}_{2}}$,${A}_{2}\overline{{A}_{1}}$互斥,B1,B2互斥,然后求出所求概率即可.
(2)顾客抽奖1次可视为3次独立重复试验,判断X~B$(3,\frac{1}{5})$.求出概率,得到X的分布列,然后求解期望.
解答 解:(1)记事件A1={从甲箱中摸出一个球是红球},事件A2={从乙箱中摸出一个球是红球},事件B1={顾客抽奖1次获一等奖},事件B2={顾客抽奖1次获二等奖},事件C={顾客抽奖1次能获奖},由题意A1,A2相互独立,${A}_{1}\overline{{A}_{2}}$,${A}_{2}\overline{{A}_{1}}$互斥,B1,B2互斥,且B1=A1A2,B2=${A}_{1}\overline{{A}_{2}}$+${A}_{2}\overline{{A}_{1}}$,C=B1+B2,因为P(A1)=$\frac{4}{10}=\frac{2}{5}$,P(A2)=$\frac{5}{10}=\frac{1}{2}$,所以,P(B1)=P(A1)P(A2)=$\frac{2}{5}×\frac{1}{2}$=$\frac{1}{5}$,P(B2)=P(${A}_{1}\overline{{A}_{2}}$)+P(${A}_{2}\overline{{A}_{1}}$)=$P({A}_{1})P(\overline{{A}_{2}})$+$P(\overline{{A}_{1}})P({A}_{2})$=$\frac{2}{5}×(1-\frac{1}{2})+(1-\frac{2}{5})×\frac{1}{2}$=$\frac{1}{2}$,故所求概率为:P(C)=P(B1+B2)=P(B1)+P(B2)=$\frac{1}{5}+\frac{1}{2}=\frac{7}{10}$.
(2)顾客抽奖1次可视为3次独立重复试验,由(1)可知,顾客抽奖1次获一等奖的概率为:$\frac{1}{5}$$\begin{array}{c},\end{array}\right.$所以.X~B$(3,\frac{1}{5})$.于是,P(X=0)=${C}_{3}^{0}(\frac{1}{5})^{0}({\frac{4}{5})}^{3}$=$\frac{64}{125}$,P(X=1)=${C}_{3}^{1}{(\frac{1}{5})}^{1}{(\frac{4}{5})}^{2}$=$\frac{48}{125}$,P(X=2)=${C}_{3}^{2}{(\frac{1}{5})}^{2}{(\frac{4}{5})}^{1}$=$\frac{12}{125}$,P(X=3)=${C}_{3}^{3}{(\frac{1}{5})}^{3}{(\frac{4}{5})}^{0}$=$\frac{1}{125}$.
故X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{64}{125}$ | $\frac{48}{125}$ | $\frac{12}{125}$ | $\frac{1}{125}$ |
点评 期望是概率论和数理统计的重要概念之一,是反映随机变量取值分布的特征数,学习期望将为今后学习概率统计知识做铺垫,它在市场预测,经济统计,风险与决策等领域有着广泛的应用,为今后学习数学及相关学科产生深远的影响.

 名校课堂系列答案
名校课堂系列答案
| A. | 1+$\sqrt{3}$ | B. | 1+2$\sqrt{2}$ | C. | 2+$\sqrt{3}$ | D. | 2$\sqrt{2}$ |
| A. | (2,3) | B. | (2,4] | C. | (2,3)∪(3,4] | D. | (-1,3)∪(3,6] |
 如图,已知圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.
如图,已知圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.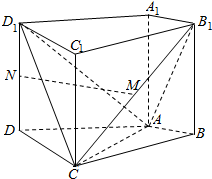 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$,且点M和N分别为B1C和D1D的中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$,且点M和N分别为B1C和D1D的中点.