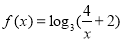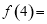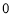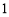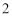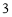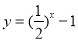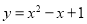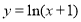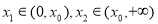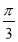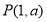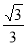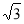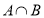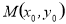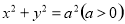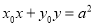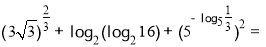题目内容
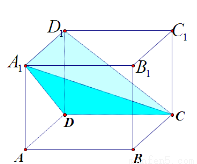
在长方体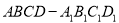
中，截下一个棱锥
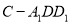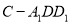，求棱锥的体积与剩余部分的体积之比．
1∶5
【解析】
试题分析：长方体看成直四棱柱ADD1A1-B1C1CB，设它的底面ADD1A1面积为S，高为h，求出棱锥C- A1D D1的体积，余下的几何体的体积，即可得到结果．
试题解析：已知长方体是直四棱柱，
设它的底面ADD1A1的面积为S，高为h， 2分
则它的体积为V=Sh． 4分
而棱锥C-A1DD1的底面积为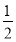
S，高为h， 6分
故三棱锥C-A1DD1的体积：
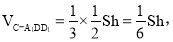8分
余下部分体积为：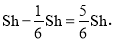
10分
所以棱锥C-A1DD1的体积与剩余部分的体积之比为1∶5． 12分
考点：棱柱、棱锥、棱台的体积．
练习册系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
相关题目
