题目内容
【题目】若数列各项均非零,且存在常数![]() ,对任意
,对任意![]() ,
,![]() 恒成立,则成这样的数列为“类等比数列”,例如等比数列一定为类等比数列,则:
恒成立,则成这样的数列为“类等比数列”,例如等比数列一定为类等比数列,则:
(1)各项均非零的等差数列是否可能为“类等比数列”?若可能,请举例;若不能,说明理由;
(2)已知数列![]() 为“类等比数列”,且
为“类等比数列”,且![]() ,是否存在常数
,是否存在常数![]() ,使得
,使得![]() 恒成立?
恒成立?
(3)已知数列![]() 为“类等比数列”,且
为“类等比数列”,且![]() ,求
,求![]() .
.
【答案】(1)可能,如![]() ;(2)存在,证明见解析;(3)
;(2)存在,证明见解析;(3)![]()
【解析】
(1)设出符合条件的等差数列,如![]() ,根据题意进行证明即可检验;
,根据题意进行证明即可检验;
(2)对![]() ,
,![]() 作差整理后可得
作差整理后可得![]() ,进而得到
,进而得到![]() ,
,![]() 即将条件中的数值代入即可求解;
即将条件中的数值代入即可求解;
(3)先根据条件解得![]() 的通项公式,再求
的通项公式,再求![]() ,可得到
,可得到![]() 为周期函数,进而得到结果
为周期函数,进而得到结果
(1)可能;设![]() 为各项均非0的等差数列,可设
为各项均非0的等差数列,可设![]() ,
,
由![]() 得
得![]() ,
,![]() 为常数,
为常数,
![]() 可得到各项均非零的等差数列为“类等比数列”
可得到各项均非零的等差数列为“类等比数列”
(2)存在常数![]() ,使
,使![]() 恒成立;
恒成立;
证明:![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,
![]() ,对等式两边同时除以
,对等式两边同时除以![]() ,得
,得![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() ,
,

![]() 存在常数
存在常数![]() ,使
,使![]() 恒成立
恒成立
(3)由题,![]() ,
,![]() ,即
,即![]()
由(2)可知![]()
![]()
![]() 、
、![]() 均为公比为
均为公比为![]() 的等比数列,
的等比数列,
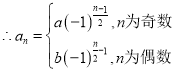 ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 是周期为4的数列,
是周期为4的数列, ![]()
![]()

练习册系列答案
相关题目