题目内容
(本小题满分14分)已知函数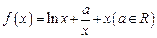 .
.
(1)求函数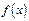 的单调区间;
的单调区间;
(2)若以函数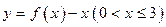 图像上任意一点
图像上任意一点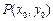 为切点的切线的斜率
为切点的切线的斜率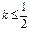 恒成立,求实数a的最小值;
恒成立,求实数a的最小值;
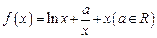 .
.(1)求函数
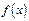 的单调区间;
的单调区间;(2)若以函数
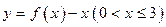 图像上任意一点
图像上任意一点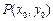 为切点的切线的斜率
为切点的切线的斜率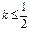 恒成立,求实数a的最小值;
恒成立,求实数a的最小值;(1)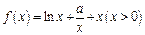 ,
,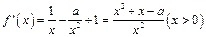 (1分)
(1分)
方程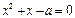 的判别式
的判别式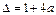
当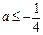 时,
时, 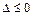
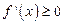
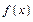 在
在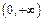 单调递增 (3分)
单调递增 (3分)
当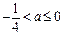 时,
时, 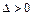 方程
方程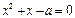 有两个根均小于等于零
有两个根均小于等于零
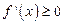
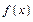 在
在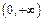 单调递增 (5分)
单调递增 (5分)
当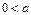 时,
时, 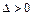 方程
方程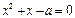 有一个正根
有一个正根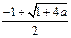 ,
,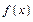 在
在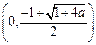 单调递减,在
单调递减,在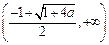 单调递增 (7分)
单调递增 (7分)
综上 当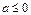 时,
时, 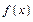 在
在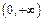 单调递增;
单调递增;
当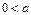 时,
时, 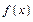 在
在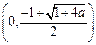 单调递减
单调递减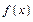 在
在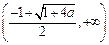 单调递增 (8分)
单调递增 (8分)
(2)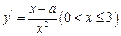 ,
,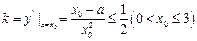 恒成立
恒成立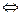
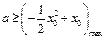
当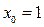 时,
时,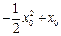 取得最大值
取得最大值 。
。
∴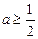 , ∴
, ∴ 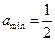 (14分)
(14分)
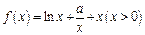 ,
,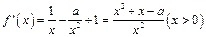 (1分)
(1分)方程
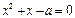 的判别式
的判别式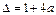
当
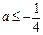 时,
时, 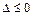
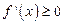
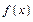 在
在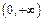 单调递增 (3分)
单调递增 (3分)当
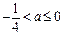 时,
时, 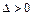 方程
方程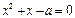 有两个根均小于等于零
有两个根均小于等于零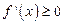
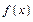 在
在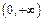 单调递增 (5分)
单调递增 (5分)当
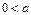 时,
时, 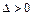 方程
方程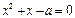 有一个正根
有一个正根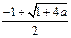 ,
,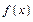 在
在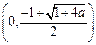 单调递减,在
单调递减,在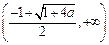 单调递增 (7分)
单调递增 (7分) 综上 当
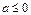 时,
时, 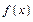 在
在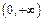 单调递增;
单调递增;当
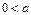 时,
时, 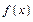 在
在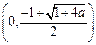 单调递减
单调递减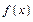 在
在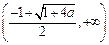 单调递增 (8分)
单调递增 (8分)(2)
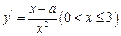 ,
,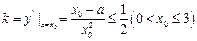 恒成立
恒成立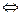
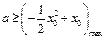
当
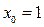 时,
时,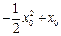 取得最大值
取得最大值 。
。∴
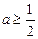 , ∴
, ∴ 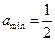 (14分)
(14分)略

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
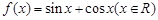 的图象按向量
的图象按向量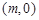 平移后,得到函数
平移后,得到函数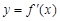 的图象,其中:
的图象,其中: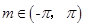 ,则
,则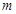 的值是___;
的值是___; 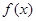 的导函数为
的导函数为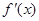 ,若对于定义域内任意
,若对于定义域内任意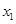 ,
,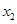
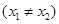 ,有
,有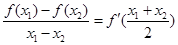 恒成立,则称
恒成立,则称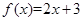 ;②
;②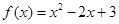 ;③
;③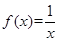 ;④
;④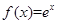 ;⑤
;⑤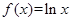 .其中为恒均变函数的序号是 .(写出所有满足条件的函数的序号)
.其中为恒均变函数的序号是 .(写出所有满足条件的函数的序号)

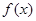 在[1,
在[1, 上递增,求
上递增,求 的取值范围;
的取值范围; 上的函数
上的函数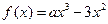 ,其中
,其中 为大于零的常数.
为大于零的常数.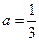 时,令
时,令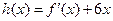 ,
, 时,
时, (
( 为自然对数的底数);
为自然对数的底数); ,在
,在 处取得最大值,
处取得最大值,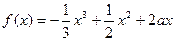 .
.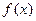 在
在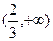 上存在单调递增区间,求
上存在单调递增区间,求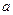 的取值范围;
的取值范围;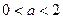 时,
时,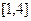 上的最小值为
上的最小值为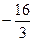 ,求
,求 ,
, ,
,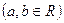
 时,若
时,若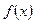 在
在 上单调递增,求
上单调递增,求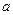 的取值范围;
的取值范围; :当
:当 ,使得
,使得 是
是 是
是 的最小值;
的最小值;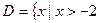 ,且
,且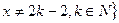 上的函数
上的函数 ,使当
,使当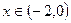 时,
时, ,当
,当 时,
时,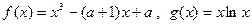 .
.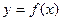 ,
,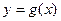 在
在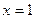 处的切线相互垂直,求这两个切线方程;
处的切线相互垂直,求这两个切线方程;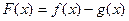 单调递增,求
单调递增,求 的取值范围.
的取值范围. 是函数
是函数 的一个极值点,其中
的一个极值点,其中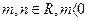
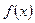 的单调区间
的单调区间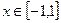 时函数
时函数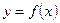 的图象上一任意点的切线斜率恒大于3m,求m的取值范围
的图象上一任意点的切线斜率恒大于3m,求m的取值范围