题目内容
已知实数x,y满足
且z=ax+y仅在点(3,2)处取得最大值,则a的取值范围是
|
(-
,+∞)
| 1 |
| 2 |
(-
,+∞)
.| 1 |
| 2 |
分析:先画出可行域,根据题中条件目标函数z=ax+y (其中a>0),仅在(3,2)处取得最大值得到目标函数所在位置,求出其斜率满足的条件即可求出a的取值范围.
解答: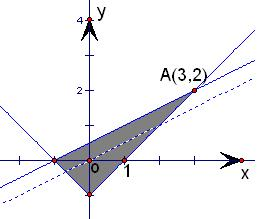 解:条件
解:条件
对应的平面区域如图:
因为目标函数z=ax+y (其中a>0),仅在(3,2)处取得最大值,
所以目标函数z=ax+y的极限位置应如图所示,
∵直线x-2y+1=0的斜率为
,
故其斜率需满足 k=-a<
?a>-
.
故答案为:(-
,+∞).
 解:条件
解:条件
|
因为目标函数z=ax+y (其中a>0),仅在(3,2)处取得最大值,
所以目标函数z=ax+y的极限位置应如图所示,
∵直线x-2y+1=0的斜率为
| 1 |
| 2 |
故其斜率需满足 k=-a<
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(-
| 1 |
| 2 |
点评:用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,以及数形结合、等价转化的思想.

练习册系列答案
相关题目
已知实数x,y满足
-
=1(a>0,b>0),则下列不等式中恒成立的是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、|y|<
| ||
B、y>-
| ||
C、|y|>-
| ||
D、y<
|