题目内容
已知定义在[-3,3]上的函数 y=tx-| 1 | 2 |
(1)当t∈[2,6]时,求f(x)在[-2,0]上的最小值及取得最小值时的x;
(2)当t≥6时,证明函数y=f(x)的图象上至少有一点在直线y=8上.
分析:(1)求出函数的导数,研究函数f(x)在[-2,0]上的单调性,确定出最值的位置,求出最值及取得最值时的自变量;
(2)t≥6时,研究函数的单调性,求出函数在定义在[-3,3]上最大值,将此最值与8比较即可得出所要证明的结论成立与否
(2)t≥6时,研究函数的单调性,求出函数在定义在[-3,3]上最大值,将此最值与8比较即可得出所要证明的结论成立与否
解答:解:(1)f'(x)=t-
x2,令f′(x)=0得x=±
∵2≤t≤6∴
∈[
,2]
当
=2时,即t=6时,f(x)在[-
,0]上是增函数,
当
<2即2<t<6时,f(x)在(-2,-
)减,在(-
,0)上增
∴f(x)在[-2,0]上最小值为f(x)min=f(-
)=-(
)
,此时x=-
=-
(2)由(1)可知f(x)在(-
,
)上增,
当
≥3即t≥
时,f(x)在[-3,3]上最大值为f(3)=3t-
≥
-
=27>8
当
<3即6≤t<
时,f(x)在[0,3]上最大值为,f(
)=t
-
(
)3=(
)
≥(
)
=8
又f(0)=0,
∴y=f(x)的图象上至少有一点在直线y=8上
| 3 |
| 2 |
|
∵2≤t≤6∴
|
|
| x | (-3,-
|
-
|
(-
|
|
(
| ||||||||||||||||||||||||
| f'(x) | - | 0 | + | 0 | - | ||||||||||||||||||||||||
| f(x) | ↘ | 极小值 | ↗ | 极大值 | ↘ |
|
|
当
|
|
|
∴f(x)在[-2,0]上最小值为f(x)min=f(-
|
|
| 3 |
| 2 |
|
|
(2)由(1)可知f(x)在(-
|
|
当
|
| 27 |
| 2 |
| 27 |
| 2 |
| 81 |
| 2 |
| 27 |
| 2 |
当
|
| 27 |
| 2 |
|
|
| 1 |
| 2 |
| 2t |
| 3 |
| 2t |
| 3 |
| 3 |
| 2 |
| 2×6 |
| 3 |
| 3 |
| 2 |
又f(0)=0,
∴y=f(x)的图象上至少有一点在直线y=8上
点评:本题考查利用导数求闭区间上的最值,解题的关键是利用导数研究清楚函数的单调性,确定出最值取到的位置,求出最值,本题第二小题将图象在直线上方的问题转化为函数值的比较,解题时注意这一技巧的运用,本题运算量比较大,解题时要注意严谨运算,莫因为运算出错导致解题失败

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
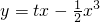 ,(t为常数).
,(t为常数).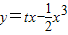 ,(t为常数).
,(t为常数).