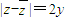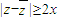题目内容
对任意复数z=x+yi(x,y∈R),i为虚数单位,则下列结论正确的是( )
A、|z-
| ||
| B、z2=x2-y2 | ||
C、|z-
| ||
| D、|z|≤|x|+|y| |
分析:求出复数的共轭复数,求它们和的模判断①的正误;求z2=x2-y2+2xyi,显然B错误;|z-
|≥2y,不是2x,故C错;|z|=
≤|x|+|y|,正确.
. |
| z |
| x2+y2 |
解答:解:可对选项逐个检查,A选项,|z-
|≥2y,故A错,
B选项,z2=x2-y2+2xyi,故B错,
C选项,|z-
|≥2y,故C错,
故选D.
. |
| z |
B选项,z2=x2-y2+2xyi,故B错,
C选项,|z-
. |
| z |
故选D.
点评:本题主要考查了复数的四则运算、共轭复数及其几何意义,属中档题

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
对任意复数z=x+yi(x,y∈R),i为虚数单位,则下列结论正确的是( )
A、|z-
| ||
| B、z2=x2+y2 | ||
C、|z-
| ||
| D、|z|≤|x|+|y| |
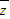 |=2y
|=2y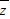 |≥2
|≥2