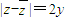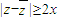题目内容
对任意复数z=x+yi（x，y∈R），i为虚数单位，则下列结论正确的是（ ）A．|z-
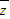|=2yB．z2=x2+y2
C．|z-
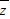|≥2D．|z|≤|x|+|y|
【答案】分析：根据|z-
|=|2yi|=2|y|，可得 A、C不正确，根据z2 =x2-y2-2xyi，可得B不正确，由|z|=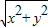
可得D正确．
解答：解：由于复数z=x+yi（x，y∈R），i为虚数单位，∴|z-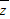
|=|2yi|=2|y|，故（A）错误．
由z2 =x2-y2-2xyi，故（B）错误．
由|z-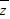
|=2|y|，不一定大于或等于2x，故（C）错误．
由|z|=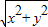
≤
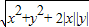=|x|+|y|，故（D）正确．
故选 D．
点评：本题考查两个复数代数形式的乘法，虚数单位i的幂运算性质，复数的模的定义，准确理解复数的模的定义，是解题的关键．
|=|2yi|=2|y|，可得 A、C不正确，根据z2 =x2-y2-2xyi，可得B不正确，由|z|=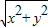 可得D正确．解答：解：由于复数z=x+yi（x，y∈R），i为虚数单位，∴|z-
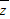|=|2yi|=2|y|，故（A）错误．由z2 =x2-y2-2xyi，故（B）错误．
由|z-
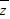|=2|y|，不一定大于或等于2x，故（C）错误．由|z|=
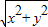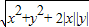≤=|x|+|y|，故（D）正确．故选 D．
点评：本题考查两个复数代数形式的乘法，虚数单位i的幂运算性质，复数的模的定义，准确理解复数的模的定义，是解题的关键．
练习册系列答案
相关题目
对任意复数z=x+yi（x，y∈R），i为虚数单位，则下列结论正确的是（ ）
A、|z-
| ||
| B、z2=x2-y2 | ||
C、|z-
| ||
| D、|z|≤|x|+|y| |
对任意复数z=x+yi（x，y∈R），i为虚数单位，则下列结论正确的是（ ）
A、|z-
| ||
| B、z2=x2+y2 | ||
C、|z-
| ||
| D、|z|≤|x|+|y| |
i),g(-1+
i),g(1+
i)，并设立它们之间的一个等式.
