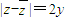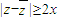题目内容
对任意复数z=x+yi(x、y∈R),定义g(z)=3x(cosy+isiny).(1)若g(z)=3,求相应的复数z.
(2)若z=a+bi(a、b∈R)中的a为常数,则令g(z)=f(b),对任意b,是否一定有常数m(m≠0)使得f(b+m)=f(b)?这样的m是否唯一?说明理由.
(3)计算g(2+![]() i),g(-1+
i),g(-1+![]() i),g(1+
i),g(1+![]() i),并设立它们之间的一个等式.
i),并设立它们之间的一个等式.
思路解析:将复数问题转化为实数问题来研究是解决复数问题的一种重要思想方法,而实现转化的桥梁是复数相等的条件.此外本题涉及到三角函数的运算.
解:(1)由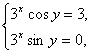 得
得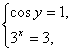 则
则![]()
故z=1+2kπi,k∈Z.
(2)由f(b+m)=f(b),得
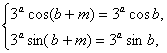 即
即![]() ∴m=2kπ,k∈Z.∴m是不唯一的.
∴m=2kπ,k∈Z.∴m是不唯一的.
(3)∵g(2+![]() i)=9(
i)=9(![]() +
+![]() i),g(-1+
i),g(-1+![]() i)=
i)=![]() (
(![]() +
+![]() i),g(1+
i),g(1+![]() i)=3i,
i)=3i,
∴g(2+![]() i)g(-1+
i)g(-1+![]() i)=g(1+
i)=g(1+![]() i).
i).

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
对任意复数z=x+yi(x,y∈R),i为虚数单位,则下列结论正确的是( )
A、|z-
| ||
| B、z2=x2-y2 | ||
C、|z-
| ||
| D、|z|≤|x|+|y| |
对任意复数z=x+yi(x,y∈R),i为虚数单位,则下列结论正确的是( )
A、|z-
| ||
| B、z2=x2+y2 | ||
C、|z-
| ||
| D、|z|≤|x|+|y| |
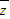 |=2y
|=2y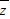 |≥2
|≥2