题目内容
（几何证明选讲选做题）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，直线MN切⊙O于D，∠MDA=60°，则∠BCD=150°
150°
．分析：利用圆的直径的性质、弦切角定理和圆内接四边形的性质定理即可得出．
解答：解：如图所示，连接BD．∵AB是圆O的直径，∴∠ADB=90°．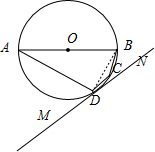
由弦切角定理可得：∠ABD=∠MDA=60°，∴∠BAD=30°．
由圆内接四边形的性质定理可得：∠BCD=180°-30°=150°．
故答案为150°．
由弦切角定理可得：∠ABD=∠MDA=60°，∴∠BAD=30°．
由圆内接四边形的性质定理可得：∠BCD=180°-30°=150°．
故答案为150°．
点评：熟练掌握圆的直径的性质、弦切角定理和圆内接四边形的性质定理是解题的关键．
练习册系列答案
相关题目
（几何证明选讲选做题）
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
（几何证明选讲选做题）
（几何证明选讲选做题）