题目内容
【题目】设函数f(x)=|ex﹣a|+| ![]() ﹣1|,其中a,x∈R,e是自然对数的底数,e=2.71828…
﹣1|,其中a,x∈R,e是自然对数的底数,e=2.71828…
(1)当a=0时,解不等式f(x)<2;
(2)求函数f(x)的单调增区间;
(3)设a≥ ![]() ,讨论关于x的方程f(f(x))=
,讨论关于x的方程f(f(x))= ![]() 的解的个数.
的解的个数.
【答案】
(1)解:当a=0时,不等式f(x)<2,即: ![]() ,
,
即 ![]() ,因此
,因此 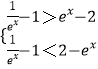
得 ![]() ,所以
,所以 ![]() ,
,
所以原不等式的解集为 ![]() .
.
(2)解:①当a≤0时, 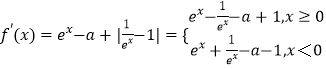
因为x>0时, ![]() ,x<0时,
,x<0时, ![]() ,
,
故f(x)在区间(﹣∞,0)上单调递减,在区间(0,+∞)上单调递增;…(5分)
②当0<a<1时, 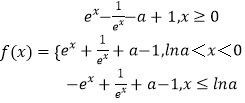 ,
,
仿①得f(x)在(﹣∞,lna)和(lna,0)上单调递减,在(0,+∞)上单调递增,
即f(x)在区间(﹣∞,0)上单调递减,在区间(0,+∞)上单调递增;(6分)
③当a=1时, 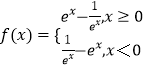
易得f(x)在区间(﹣∞,0)上单调递减,在区间(0,+∞)上单调递增; …(7分)
④当a>1时, 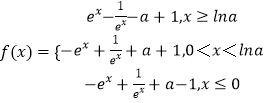
同理得f(x)在区间(﹣∞,lna)上单调递减,在区间(lna,+∞)上单调递增.…(8分)
综上所述,
当a≤1时,f(x)在区间(﹣∞,0)上单调递减,在区间(0,+∞)上单调递增;
当a>1时,f(x)在区间(﹣∞,lna)上单调递减,在区间(lna,+∞)上单调递增.…(10分)
(3)解:由(2)知:当 ![]() 时,因为
时,因为 ![]() ,
,
又x→+∞时, ![]() ,
,
所以f(x)的值域为 ![]() ,且
,且 ![]() (等号仅当
(等号仅当 ![]() 时取).)
时取).)
令 ![]() ,
,
当 ![]() 时,
时, ![]() ,所以
,所以 ![]() 不成立,原方程无解;
不成立,原方程无解;
当 ![]() 时,由
时,由 ![]() 得
得 ![]() ,因为
,因为 ![]() ,所以
,所以 ![]() ,
,
所以 ![]() 有两个不相等的实数根,故原方程有两个不同的实数解.
有两个不相等的实数根,故原方程有两个不同的实数解.
综上所述,当 ![]() 时,原方程无解;当
时,原方程无解;当 ![]() 时,原方程有两个不同的实数解.
时,原方程有两个不同的实数解.
【解析】(1)将a=0代入不等式,得到关于x的不等式组,解出即可;(2)通过讨论a的范围,求出f(x)的分段函数,从而求出函数的单调区间;(3)先求出函数的值域,结合换元法以及a的范围,求出方程的解即可.
【考点精析】掌握绝对值不等式的解法是解答本题的根本,需要知道含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案